|
| Les cases correspondantes par Ta***le*9631 le
[Aller à la fin] |
| Théorie | |
Ce sujet a été traité dans:
« L'opposition et cases conjuguées sont réconciliées », par Vitaly Halberstadt and Marcel Duchamp.
Pourrait-on, en s'y prenant bien, enseigner cela à l'école primaire comme exercice de logique?
La numérotation des cases n'est pas toujours évidente et il faut d'abord comprendre les cases-clés.
L'article de wikipedia en anglais sur ce thème est assez riche, mais vide en français.
Ce qui me fait rire est que les joueurs n'ont pas le droit de prendre des notes pendant une partie. Ils seraient alors disqualifiés s'ils dessinaient des petits diagrammes avec des chiffres?
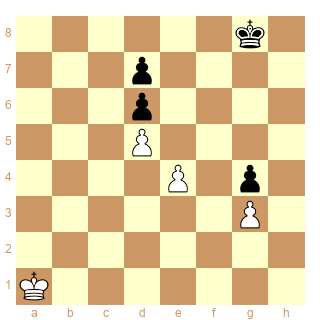
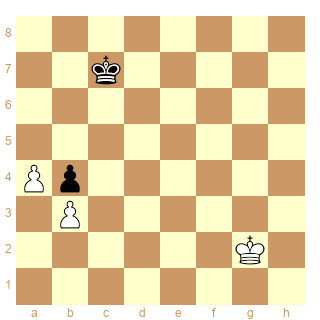
Diagramme les Blancs jouent et gagnent.
|
|
Le java ne passe pas pour une raison que j'ignore (peut-être un divin modérateur pourrait-il rectifier cela?)
Les coups sont : 1.Rb1 Rg7 2.Rc1 Rg6 3.Rd1 Rg5 4.Rc2 Rh5 5.Rc3 Rg5 6.Rc4 Rg6 7.Rd3 Rg5 8.Rd4
Tous les coups des Blancs sauf le dernier sont uniques.
|
|
|
Sans doute parce qu'il n'y a aucune entête, ni résultat dans le pgn.
|
|
|
Et c'est Re3 au 8ème coup...
|
|
|
Le pgn que j'ai posté:
[Event "?"]
[Site "?"]
[Date "2012.08.29"]
[Round "?"]
[White "Nouvelle partie"]
[Black "?"]
[Result "*"]
[SetUp "1"]
[FEN "6k1/3p4/3p4/3P4/4P1p1/6P1/8/K7 w - - 0 0"]
[PlyCount "15"]
1. Kb1 Kg7 2. Kc1 Kg6 3. Kd1 Kg5 4. Kc2 Kh5 5. Kc3 Kg5 6. Kc4 Kg6 7. Kd3 Kg5 8.
Kd4 *
@Petieglise:
oui c'est c'est Re3 au 8ème coup...
il y en a qui suivent!
|
|
|
Oui, c'est Re3 suivi de Rf4 pour les blancs
|
|
|
Si quelqu'un connait d'autres finales de pions qui peuvent être résolues par les cases conjuguées, je suis intéressé.
|
|
|
Le volume 1 des finales de Villeneuve en regorge !
|
|
|
Il y a bien cette étude (1901) composée par le chamion du monde Emmanuel Lasker et Gustavus Charles Reichhelm.
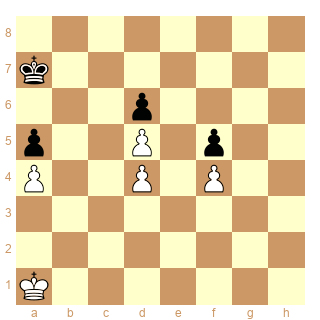
Diagramme: les Blancs jouent et gagnent
(1.Rb1 Rb7 2.Rc1 Rc7 3.Rd1 Rd8 4.Rc2 Rc8 5.Rd2 Rd7 6.Rc3 Rc7 7.Rd3 Rb6 8.Re3+-)
mais elle a déjà été postée.
|
|
|
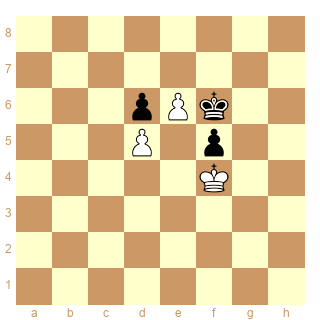
Encore cette étude de Grigoriev 1924, Les Blancs jouent et font nulle:
Grigoriev=N - (=0000.12c5d8)
Isvestia#109, 29.11.1924
1.Rc6! [1.Rd6? Re8 2.Re5 Rd7] 1...Rc8 2.Rd6 Rd8 3.Rc6 Re8 4.Rd6 Rf8 5.Re5 Rg8 6.Rf4 Rh7 7.Rg5! Rh8 8.Rg4! Rg8 [8...e5 9.Rf5 Rh7 10.Rxe5 Rg6 11.Re4! Rxf6 12.Rf4] 9.Rf4! ½-½

|
|
|
@tantale
Il y a un bouquin russe dont j'ai oublié le nom qui en parle de manière assez exhaustive. Correspondances entre 3 cases et plus. Je peux essayer de me renseigner pour retrouver le titre si tu veux.
Sinon il y a un petit bouquin en anglais de Willem Hajenius et Herman van Riemsdijk qui s'appelle The final countdown.
|
|
|
@Ofkrad merci.
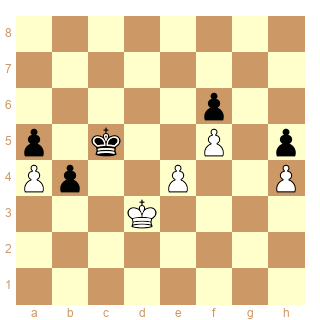
Dans cette position la théorie des cases conjuguées semble dire que le Roi blanc doit obligatoirement passer par la case g2 pour gagner. Est-ce exact.
|
|
|
Oui. Les oppositions sont f4 f6 et h4 g6. Si on descend h3 f6, g3 g6 et f3 g6. L'opposition à g2 est f7 non accessible aux noirs. Il faut aller sur g2 et prendre l'opposition en fonction du coup noir.
|
|
|
Il y a la position Seirawan Kasparov Niksic 83 qui montre bien les cases conjuguées.
|
|
|
voici un lien plus ancien mais intéressant traitant des cases conjuguées également
|
|
|
Merci Torlof
J'ai sans doute écrit "cases correspondantes" au lieu du terme plus précis "cases conjuguées" sous l'influence de l'anglais "corresponding squares"
|
|
|
Encore une vidéo (en anglais) qui explique les cases conjuguées à partir d'une étude de Grigoriev.
|
|
|
par ailleurs on trouve ici un étonnant développement d'un certain Kloch qui vaut vraiment le détour pour l’exhaustivité et la maîtrise de son exposé!
à cette source Tantale devrait pouvoir remplir son vase !
j'insiste, car c'est monstrueux sur le plan de l'effort didactique : ça débute vraiment à : Kloch, le 31/07/2007 - 02:49:38
par ailleurs : "cases correspondantes" & "cases conjuguées" sont vraiment des termes jumeaux ici, à mon sens, et je pense qu'il peuvent être utilisés indifféremment. ( juste mon avis :)
|
|
|
@torlof
Je me souviens d'une fois ou Lupu n'avait pas pu venir donner son cours au Chess XV. Nikolay Yordanov nous avait dit: tenez, je viens de lire un truc génial dans un livre russe sur les cases conjuguées. Au bout de 15mn d'explications sur comment reperer et nommer les cases, tout le monde du 1700 au 2200 trouvait la solution en moins de 30 secondes. Aucun besoin de calcul, il suffisait juste de repérer la case sans correspondance du camp adverse.
|
|
|
@Torlof
Merci beaucoup pour ce lien qui semble très intéressant et que je vais potasser demain.
Je sens que je vais prendre 100 points elo.
|
|
|
@Tantale 100 points elo c'est toujours possible mais du plaisir c'est une certitude!
@Ofkrad merci pour l'anecdote! elle prouve que l'esprit humain nous place au dessus des tables bas(s)es.
|
|
|
Pour répondre à la toute première suggestion de Tantale, il me semble que la position initiale risque d'être un peu ardue pour la plupart des élèves de primaire; des finales plus élémentaires à base d'opposition me paraissent plus adaptées.
En revanche toutes ces finales de pions bloqués avec conjugaison se prêtent assez bien à une résolution utilisant des représentations empruntées à la théorie des graphes, un peu comme le problème des ponts de Königsberg d'Euler. Je laisse les plus matheux gamberger sur ça.
En ce qui concerne la littérature relative à la conjugaison dans les finales de Pions (la conjugaison existe aussi pour les autres pièces, aussi bien entre pièces homologues qu'hétérologues), erony sera sans doute le plus qualifié pour te répondre.
Pour ma part il me semble que la plupart des bouquins de finales de Pions traitent ces notions. Le plus complet à ma connnaissance est le Comprehensive Chess Endings (Averbakh) avec un chapitre spécifique de Zinar sur le sujet. Le bouquin russe indiqué par Ofkrad est peut-être celui d'Averbakh et Maizelis. En français (pas toujours bien traduit/corrigé et difficile à trouver) il y a justement le Finales de Pions (Maizelis).
|
|
|
Puisqu'il passe par ici, j'en profite pour remercier Kloch pour son excellent article :o)
|
|
|
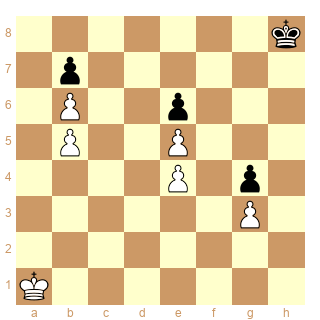
Quel est le seul coup gagnant des Blancs dans cette position?
J'ai lu l'article de Kloch et définitivement je pense que le sujet des cases conjuguées dépasse le niveau de l'école primaire.
Je pensais qu'une fois les cases clés déterminées il sufisait de numéroter les cases de proche en proche mais c'est beaucoup plus complexe.
|
|
|
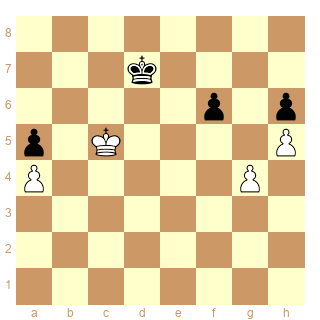
J'ai trouvé encore cet exemple où le ballet commence par :
1.Re3 Rd7 2.Rd3 Re6 3.Re4 Re7 4.Rd5 Rd7 5.Rc5 1-0
|
|
|
@Tantale
Peut-être pourrait-on plutôt dire que savoir ce que sont les cases conjuguées est simple, mais que tout savoir à leur propos ne l'est pas et qu'il existe des cas difficiles à résoudre.
Il s'agit finalement d'un sujet accessible à tous et utile à aborder.
|
|
|
Pierre Antoine Cathignol s'est fait une spécialité des duels entre deux pièces, ce qui utilise les cases conjuguées...
Pierre Antoine Cathignol
Diagrammes n°151
4+6: #28

|
|
|
@Slucaino
D'accord avec toi Déterminer les cases conjuguées n'est pas difficile et suffit pour résoudre certaines positions. Pour d'autres comme celle traitée par Kloch c'est simplement une base à partir de laquelle il faut encore beaucoup travailler pour arriver à une conclusion.
|
|
|
Ce sujet est tout-à-fait abordable et son étude, même pendant un temps court, profitable. Pourtant, il semble que de nombreux joueurs aient des réticences pour s'y intéresser, et je me demande pourquoi. Est-ce le nom qui dérange ? l'impression que cela survient dans les compositions mais pas dans les parties ? La frayeur ressentie une fois en voyant dans un livre un échiquier presque vide de pièces mais rempli de cases numérotées ? Ou encore autre chose ?
|
|
|
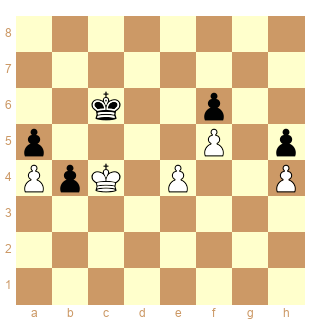
Yasser Seraiwan - Garry Kasparov 1983 - 0-1
48... Rc7! 49.Rd3 Rd7! 50.Re3 Rc6 51.Rd3 Rc5 52.Re3 b3 53.Rd3 Rb4 54.e5 Ra3! 0-1
Le gain passait-il par la compréhension des case conjuguées?
|
|
|
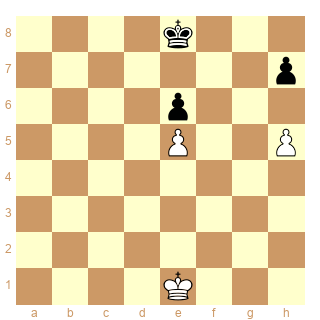
Et cette étude de Grigoriev nécessite-t-elle les cases conjuguées pour être résolue?
Les Blancs jouent et font nulle.
1.Rf2 Rd7 2.h6 Rc6 3.Rg3 Rd5 4.Rh4 Rd4 5.Rh5 Re4 6.Rg4 Rxe5 7.Rg5 Rd6 8.Rf6 ½-½
|
|
|
Dans chesscafe on trouve l'analyse de la position (trait aux Noirs) issue de la partie Ree - Ftanick 1-0 1978 que Ftanick aurait pu gagner s'il avait connu la théorie des cases conjuguées.
(Analyse de Mark Dvoretsky dans "Tragicomedies in Pawn Endings" , présentée par Karsten Müller.)

|
|
|
Kasparov a bien gagné grâce aux cases conjuguées, même si la liberté des pions e4 et b4 complique la situation et nécessite un calcul précis.
Un coup plus tôt, le Roi noir se trouvait en c5 et le blanc en d3, sa seule case. Les cases c5 et d3 sont conjuguées.
Les cases d6 et d4 sont conjuguées aussi.
La case c6 et conjuguée avec c4 ou e3.
Lorsque le Roi noir se trouve en d7 ou c7, il menace d'aller en c6 ou d6 et le Roi blanc ne doit se trouver ni en c4, ni en d4, ni en e3 mais être prêt à s'y rendre, c'est-à-dire qu'il doit être en d3. Le Roi noir n'a qu'à attendre un coup entre c7 et d7 pour que les Blancs se trouvent en Zugzwang. Tout cela se voit bien dans le déroulement de la partie.
|
|
|
Correction du diagramme ci-dessus :
Merci Slucaino je vais étudier ton analyse.

|
|
|
Comme livre sur les finales j'hésite entre les Villeneuve ou le Dvoretsky. Que me conseillez-vous?
|
|
|
La critique du Dvorestsky par l'auteur des Villeneuve pour eclairer ton choix ? :)
http://www.mjae.com/Villeneuve-Dvoretzky.html
|
|
|
Merci Bibifroc pour ce lien écrit dans un style fleuri.
|
|
|
sinon ta plusieurs fils qui en parlent plus ou moins : http://www.france-echecs.com/article.php?art=20051109132707561
et
http://www.france-echecs.com/article.php?art=20101028203635249
|
|
|
Cette étude d'Aliev et Salehov 2010 - Les Blancs jouent et font nulle - peut sans doute être comprise grâce aux cases conjuguées.
1.Rb1 Rh2 2.Rb2 Rh3 3.Rb3 Rg2 4.Rc2 Rg3 5.Rc3 Rg2 6.Rc2 Rg1 7.Rc1 Rh1 8.Rb1 Rg2 9.Rc2 Rf2 10.Rb2 Rf1 11.Rb1 Re2 12.Rc2 Rf3 13.Rb3 Rf2 14.Rb2 Re1 15.Rc1 Re2 16.Rc2 Re3 17.Rc3 ½-½

|
|
|
il existe un gros dual puisque 1.Rc3! annule aussi ( 1... Rh2 2.Rb2 ...)
on pourrait proposer la correction suivante:
 Les Blancs jouent et font nulle après Aliev et Salehov 2010 Les Blancs jouent et font nulle après Aliev et Salehov 2010
solution identique mais ici 1.Rb1! est unique
|
|
|
@Torlof
Mois je vois dans le diagramme initial 1.Rc3 Rg1! 2.Rc2 Rg2 3.Rc3 Rf1 4.Rb2 Rf2 5.Rb3 Re1 6.Rc3 Rd1 7.Rb2 Rd2-+
|
|
|
Et ne faut-il pas encore les cases conjuguées pour comprendre cette étude d'Ibrahim Aliev et Shakhriyar Mamedyarov 2008 - Les Blancs jouent et font nulle.
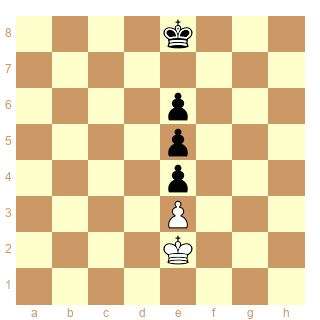
|
|
|
@Tantale tu as raison, j'ai fait une erreur de diagramme ! dsl!
|
|
|
J'ai téléchargé le bouquin de Dvoretsky sur Amazon (la version électronique est moitié prix de la version papier). Je ferai l’acquisition des Villeneuve sans doute plus tard.
Voici le premier exemple de cases conjuguées que je trouve:
Les Noirs jouent et les Blancs gagnent.
1...Rb7 2.Rb3 Ra6 3.Rb4 Rb7 4.Rc4 Ra6 5.Rd3! Ra5 6.Re4 Rb5 7.Rd4 Ra5 8.Re5 Ra4 9.Rd6 Rxa3 10.Rxc6 1-0

|
|
|
Trouvé dans le même bouguin la position:
Les Blancs jouent et annulent.
1.Rd3 Rh6 2.Rd4 Rg6 3.Re4 Rh5 4.Rd5 Rh4 5.Rd4 Rg3 6.Re3 Rh2 7.Rd2 etc ½-½
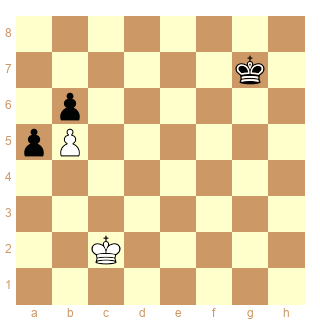
|
|
|
C'est pas plutôt 1.Rc3 ? (sinon sur 1.Rd3 il devrait y avoir Rf7)
|
|
|
@Petieglise
Sur 1.Rc3 il y a 1...Rg6!-+
Sur 1.Rd3 Rf7 2.Re3!=
|
|
|
Juste pour aider un peu Tantale avec la position de pions bloqués proposée le 30/08/2012 - 20:33:51, essayons d’appliquer le procédé que j’avais posté il y a 5 ans
Pour mieux suivre, je conseille à nouveau aux néophytes motivés de s'aider d'un diagramme et d'y annoter les cases conjuguées.
"Repérer les Cases de Pénétration"
Il faut tout d'abord repérer les cases de pénétration pour chaque camp, souvent assorties d'un gain de Pion.
Le Roi Blanc peut pénétrer par d6 et f4 alors que le Roi Noir ne dispose d’aucune case de pénétration et est simplement enfermé dans son camp.
Cette simple constatation (2 cases de pénétration contre aucune) suffit pour conclure que les Noirs n’auront pas mieux que la nulle et que seuls les Blancs ont des chances de gain.
"Attention à la Contre-Attaque"
Cette mise en garde n’est plus pertinente ici puisque les Noirs sont contraints de subir le jeu. Il n’en reste pas moins que les Blancs doivent malgré tout jouer très précisément pour ne pas laisser échapper le gain.
"Etablir les Positions de Zugzwang Réciproque"
Après avoir repéré les cases de pénétration du camp de l'attaque (= cases d6 et f4 pour le Roi Blanc), il faut établir les positions de zugzwang réciproque autour de ces cases, c-à-d les positions respectives des Rois autour de ces cases qui permettent effectivement soit au Roi Blanc de pénétrer au coup suivant et de gagner un Pion si les Noirs ont le trait, soit au Roi Noir de défendre la case si les Blancs ont le trait.
- Concernant la case d6, son occupation par le Roi Blanc garantit le gain du Pion Noir e6. Le Roi Blanc ne peut y accéder que depuis c5, et le Roi Noir la contrôle depuis d7 ou e7, mais il est bien sûr préférable pour la défense de privilégier la case la moins éloignée du second point de pénétration (c-à-d e7).
Il découle de ceci la position de zugzwang réciproque à l’Aile-Dame : Roi Blanc en c5 et Roi Noir en e7
- Concernant la case f4, les choses sont un peu plus subtiles qu’il n’y paraît. On pourrait se contenter de considérer que depuis g5 le Roi Noir peut tenir en respect le Roi Blanc en e3. C’est vrai sur le plan formel, mais ce n’est ni nécessaire, ni recommandable.
En effet, on peut noter tout d’abord (contrairement à ce qu’on vient de voir pour la case d6 et le Pion e6) que même si f4 est un passage obligé pour le Roi Blanc s’il veut gagner le Pion noir g4, le Roi Noir peut alors encore le défendre depuis h5, auquel cas le Roi Blanc doit effectivement reculer en e3.
Par ailleurs, les deux cases de défense g5 et h5 sont à 3 coups de la case e7, alors que pour le Roi Blanc, les cases e3 et f4 sont respectivement à 2 et 3 coups de la case c5. La défense Re3/Rg5 ne convient donc pas puisque le Roi Blanc aura alors le temps de pénétrer par d6.
Il découle de ceci la position de zugzwang réciproque à l’Aile-Roi : Roi Blanc en f4 et Roi Noir en h5
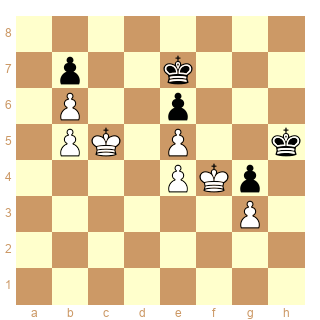
En d'autres termes, les cases c5 et e6 sont conjuguées, ainsi que les cases f4 et h5.
Cela signifie que leur occupation simultanée par les Rois avec le trait à l'adversaire est synonyme de gain d’un Pion pour les Blancs (trait aux Noirs) ou de nulle pour les Noirs (trait aux Blancs)
"Etablir le Chemin le Plus Court"
Il faut ensuite établir le Chemin le plus court entre ces cases de zugzwang réciproque, ce qui a en fait déjà été effectué précédemment puisque la détermination du chemin le plus court et la détermination des positions de zugzwang réciproque aux extrémités de ce chemin sont largement interdépendantes dans le présent exemple.
Pour les Blancs : c5-d4-e3-f4 (4 cases)
Pour les Noirs : e7-f7-g6-h5 (4 cases)
Quand le chemin du camp de l'Attaque est plus court que celui de la Défense, la victoire est en général triviale.
Ici les chemins sont de même longueur (4 cases), ce qui implique la conjugaison entre les cases équidistantes de chaque extrémité du chemin.
C-à-d notamment :
- conjugaison entre d4 et f7
- conjugaison entre e3 et g6
"Recherche de Nouvelles Cases Conjuguées"
L'étape suivante consiste à établir de proche en proche de nouvelles paires de cases conjugués en recherchant de préférence
- à établir des correspondances non dégénérées ou non-ambiguës (en tout cas pour le camp de la Défense).
- à étendre le réseau de cases conjuguées le plus possible vers la zone où se trouvent les Rois afin de trouver le "bon" coup (quand il existe).
Pour trouver de nouvelles cases conjuguées, la méthode standard consiste à rechercher des cases contiguës communes aux cases déjà identifiées.
Par exemple dans le camp Blanc, d4 et e3 ont une seule case contiguë commune accessible au Roi Blanc : d3
Dans le camp Noir, f7 et g6 (les cases conjuguées de d4 et e3) ont une seule case contiguë commune accessible au Roi Noir : g7
Conclusion : d3 et g7 sont conjuguées
Les cases d4-e3-d3/f7-g6-g7 constituent le triangle basal du système de conjugaison. Dans la position de Reichhelm/Lasker, on avait vu qu’on pouvait étendre ce triangle pour obtenir un système de conjugaison du type Triangle-Carré. Nous allons voir qu’ici la zone de conjugaison principale peut être étendue sensiblement plus pour obtenir un système de conjugaison à 8 cases, ainsi répertorié par les théoriciens des cases conjuguées tels que Zinar.
Poursuivons donc le raisonnement (pour lever certaines ambiguïtés, il est parfois nécessaire de chercher des cases contiguës à plus de 2 cases déjà identifiées) :
- les cases c5, d4 et d3 ont une seule case contiguë commune accessible au Roi Blanc : c4
- de même : les cases e7, f7 et g7 ont une seule case contiguë commune accessible au Roi Noir : f8
Conclusion : c4 et f8 sont conjuguées
- les cases d4, d3 et c4 ont une seule case contiguë commune accessible au Roi Blanc : c3
- de même : les cases f7, g7 et f8 ont une seule case contiguë commune accessible au Roi Noir : g8
Conclusion : c3 et g8 sont conjuguées
- les cases c3, d3 et e3 ont une seule case contiguë commune accessible au Roi Blanc : d2
- de même : les cases g8, g7 et g6 ont une seule case contiguë commune accessible au Roi Noir : h7
Conclusion : d2 et h7 sont conjuguées
- les cases c3, d3 et d2 ont une seule case contiguë commune accessible au Roi Blanc : c2
- de même : les cases g8, g7 et h7 ont une seule case contiguë commune accessible au Roi Noir : h8
Conclusion : c2 et h8 sont conjuguées
- les cases d3, e3 et d2 ont une seule case contiguë commune accessible au Roi Blanc : e2
- de même : les cases g7, g6 et h7 ont une seule case contiguë commune accessible au Roi Noir : h6
Conclusion : e2 et h6 sont conjuguées
On a ainsi obtenu dans les deux camps un réseau de 8 cases conjuguées présentant la même structure (une sorte de carré 3x3 tronqué), d’où le nom déjà mentionné de système de conjugaison à 8 cases qui est en fait une extension du système de conjugaison du type Triangle-Carré.
|
|
|
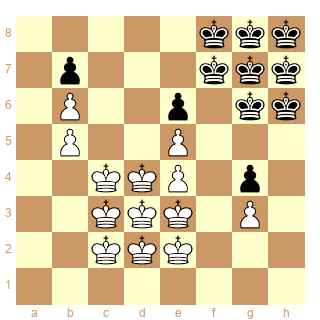
Dans ce système, les cases sont habituellement numérotées de 1 à 8 de la façon suivante, en commençant par les 3 cases du triangle basal :
1 = d4/f7
2 = e3/g6
3 = d3/g7
4 = c4/f8
5 = c3/g8
6 = c2/h8
7 = d2/h7
8 = e2/h6
"Zone de Conjugaison Principale"
L'ensemble des ces 8 cases définit en fait la zone de conjugaison principale à laquelle on peut éventuellement adjoindre les 2 cases correspondant aux positions extrêmes du "chemin le plus court" (c-à-d les positions de zugzwang réciproque identifiées en début de processus).
"Report de numérotation - Zone de Conjugaison Secondaire "
On peut alors étendre la Zone de Conjugaison Principale pour constituer une Zone de Conjugaison Secondaire en bordure du Carré tronqué de la zone principale en utilisant une règle simple souvent employée et consistant à répéter la numérotation déjà établie dans le Carré en la reportant sur des cases situées à des distances correspondant à "l'opposition directe".
On peut noter que les Noirs ne disposant d’aucun contre-jeu, il est possible d’étendre le réseau secondaire aussi loin que possible de la zone de conjugaison principale.
Pour être plus clair, en étendant vers la gauche du carré tronqué, on peut attribuer à b4 le chiffre "1", comme pour la case "mère" d4.
De même,
- b3 aura le chiffre "3" comme la case "mère" d3
- b2 aura le chiffre "7" comme la case "mère" d2
- a4 aura le chiffre "4" comme la case "mère" c4
- a3 aura le chiffre "5" comme la case "mère" c3
- a2 aura le chiffre "6" comme la case "mère" c2
De même en étendant vers le bas du carré tronqué :
- c1 aura le chiffre "5" comme la case "mère" c3
- d1 aura le chiffre "3" comme la case "mère" d3
- e1 aura le chiffre "2" comme la case "mère" e3
Il suffit de compléter les deux dernières cases vers le coin de l’échiquier :
- b1 aura le chiffre "3" comme la case "mère" d3 ou comme les cases "filles" d1 ou b3
- a1 aura le chiffre "5" comme la case "mère" c3 ou comme les cases "filles" c1 ou a3
Remarques :
- certains auteurs préfèrent la nomenclature "2a", "3a", etc., pour distinguer les cases de la zone secondaire de celles de la zone principale.
- une des raisons "géométriques" pour lesquelles ce procédé de report de numérotation toutes les 2 cases fonctionne à partir de cases adjacentes est que les nouvelles cases (cases "filles") ainsi définies, sont toujours contiguës de cases portant les mêmes chiffres que les cases voisines de la case "mère" dans la zone principale.
Exemple :
- b2 (case "fille" "7", ou case "7a") est contiguë de cases numérotées "3" sur la même colonne ou numérotées "6" ou "5" sur la colonne voisine.
- la case d2 (case "mère" "7") a les mêmes propriétés.
Dans le cas présent, la détermination de cases conjuguées secondaires dans le camp des Noirs n’a pas d’objet, puisque tout l’espace est occupé par la zone principale. Le point suivant a par conséquent peu d’intérêt ici, en tout cas en ce qui concerne la défense. Je le répète néanmoins pour sa portée générale.
"Toujours préférer la Zone Principale à la Zone Secondaire"
Il convient de noter une règle essentielle : il est toujours préférable d'occuper la zone principale.
- Du point de vue de laDéfense on peut même ajouter que si le Roi Blanc est dans la zone principale, le Roi Noir doit obligatoirement occuper la case conjuguée de la zone principale et non une case conjuguée de la zone secondaire
- Du point de vue de l'Attaque, cette règle est également valable, et à la première occasion le Roi Blanc devra rentrer dans la zone principale avec la conjugaison ou alors en s'assurant que le Roi Noir ne peut pas la récupérer (voir plus loin la Manœuvre de Débordement).
Récapitulons à nouveau les cases conjuguées en ajoutant les cases secondaires entre parenthèses :
1 (1a) = d4 (b4) / f7
2 (2a) = e3 (e1) / g6
3 (3a) = d3 (b1-b3-d1) / g7
4 (4a) = c4 (a4) / f8
5 (5a) = c3 (a1-a3-c1) / g8
6 (6a) = c2 (a2) / h8
7 (7a) = d2 (b2) / h7
8 (8a) = e2 / h6
Ce système de cases conjuguées permet déjà de trouver la solution de l'étude (sans avoir eu à calculer la moindre variante).
En effet, le Roi Noir se trouve en h8, c-à-d sur une case "6". Le Roi Blanc peut lui-même atteindre une case "6" : la case a2 (en réalité une case "6a").
D'où la clé : 1.Ra2! et non 1.Rb2? (case "7a") sur quoi les Noirs annulent par 1...Rh7!! (case "7") comme il est facile de le comprendre car les Noirs prennent la conjugaison dans la zone principale et ne la lâchent plus.
"Le Plan d'Attaque"
Après 1.Ra2! , les Blancs doivent conserver la conjugaison dans le système établi précédemment (ou en tout cas ne pas la concéder), en cherchant dans un premier temps à passer de la zone secondaire à la zone principale (= le Carré tronqué), pour ensuite progresser dans ce Carré en direction du triangle basal (cases d4-e3-d3) et surtout des cases du "chemin le plus court" (cases d4-e3).
"Manœuvre du Saut opportun ou de Débordement ou de Contournement"
Le passage de la zone secondaire à la zone principale puis la progression dans la zone principale ne sont pas toujours possibles en se contentant d'occuper les cases conjuguées de celles occupées par le Roi Noir.
Au contraire, sur une défense tenace on ne progresse qu’en renonçant provisoirement à la conjugaison mais tout en ne la concédant pas. Ceci s’obtient en contournant le Roi adverse par une case dont la case conjuguée est trop éloignée de lui (le plus souvent à 2 cases, soit en opposition, soit à un saut de Cavalier).
Cette règle, dont la signification sera je l'espère mieux comprise dans ce qui va suivre, est essentielle pour progresser dans tout système de cases conjuguées.
Examinons une suite possible pour expliciter ce qui précède (entre parenthèse figure le numéro de la case conjuguée) :
1.Ra2! ("6a") Rg8 ("5")
2.Ra3! ("5a") Rf8 ("4")
Jusqu'ici le Roi Blanc s'est contenté de conserver la conjugaison dans la zone secondaire en longeant la zone principale, faute de pouvoir s’en rapprocher sous peine de perdre la conjugaison.
Les Blancs doivent maintenant jouer de façon plus subtile pour progresser en ayant recours à la "Manœuvre de Débordement".
Jouer 3.Ra4 ("4a") conserverait en effet la conjugaison mais après 3...Rg8 ("5") on se trouve dans une impasse car les Blancs doivent à nouveau rejouer 4.Ra3 ("5a") pour conserver la conjugaison (et plus précisément pour ne pas la concéder). Or après 2…Rf8, on observe que le Roi Noir se trouve sur une case voisine des cases "1", "3" et "5", mais surtout qu'il est à 2 pas des cases "2", "6", "7" et "8". De son côté, le Roi Blanc en a3 se trouve sur une case voisine des cases "6a" (a2) et "7a" (b2).
Pour progresser, le Roi Blanc doit donc saisir l'occasion de se rapprocher de la zone principale par b2 ("7a") car le Roi Noir n'a pas la possibilité d'occuper la case conjuguée h7 ("7") trop éloignée.
Remarque importante : le débordement/contournement intervient en général juste après avoir obtenu la conjugaison sur une des traverses principales de la zone de conjugaison, c-à-d sur les lignes médianes du carré tronqué à 8 cases qui portent le triangle basal (3ème rangée ou colonne d pour les Blancs, respectivement colonne g ou 7ème rangée pour les Noirs). En effet, une fois sur ces lignes médianes, le Roi Noir n’a que le choix de reculer sur cette ligne (mais le Roi Blanc avancera directement en conservant la conjugaison), ou de s’écarter en bordure de la zone, mais le Roi Blanc en profitera alors pour se rapprocher des cases basales en contournant le Roi Noir par la bordure opposée et en allant ainsi sur une case dont la case conjuguée est trop éloignée de celui-ci.
Cette phase du jeu équivaut dans le système plus simple d'opposition directe autour de 3 cases-clés contiguës, à l'étape de contournement par le Roi autour de la case-clé centrale pour s'emparer d'une case-clé latérale. Ici le contournement s’opère simplement à distance (mais si cette allusion vous échappe, oubliez-la).
D'où la suite 3.Rb2 après 2...Rf8 : en effet, en passant de g8 à f8, le Roi Noir a quitté une des traverses principales de la zone de conjugaison à 8 cases (ici il a quitté la colonne g). Dans le camp Blanc, cette traverse correspond à la 3ème rangée sur laquelle se trouvait le Roi Blanc (Ra3). En essayant de visualiser le déplacement du Roi Noir dans la zone de conjugaison des Blancs, on voit bien que le Roi Noir est passé de la case conjuguée de c3 (g8) à la case conjuguée de c4 (f8). Le Roi Noir ayant quitté la traverse principale, c’est le moment pour le Roi Blanc de le contourner (à distance) par la 2ème rangée.
D’où le coup 3.Rb2! ("7a")
Maintenant le Roi Noir a le choix suivant :
A) 3...Re8(e7), est évidemment inconséquent et le Roi Blanc entre sans souci dans la zone principale par exemple par 4.Rc3
B) sur 3...Rg8 ("5"), le Roi Blanc joue 4.Rc3! ("5") et rentre dans la zone principale tout en conservant la conjugaison
C) sur 3... Rf7 ("1"), le Roi Noir reste en bordure de la zone de conjugaison et ne revient pas sur la traverse principale (colonne g); le Roi Blanc peut donc poursuivre sa manœuvre de contournement le long de la bordure opposée (2ème rangée) et joue donc4.Rc2! ("6") qui lui permet d’entrer dans la zone principale sans obtenir la conjugaison mais sans la concéder non plus, la case "6" (h8) n’étant pas accessible au Roi Noir (voir variante D3)
D) 3...Rg7 ("3"), le Roi Noir regagne la traverse principale; les Blancs doivent donc tout d’abord récupérer la conjugaison avant de pouvoir poursuivre leur progression par contournement : 4.Rb3! ("3a")
Les Noirs ont à nouveau un choix difficile :
D1) 4...Rf8(g8-h8) ("4-5-6"), concède la conjugaison dans la zone principale par 5.Rc4(c3-c2)! ("4-5-6")
D2) 4...Rg6 ("2"), recule sur la traverse principale, et permet donc au Roi Blanc d’y avancer par 5.Rc3! ("5") sans concéder la conjugaison. Pour empêcher ensuite les Blancs de pénétrer directement par c5, les Noirs doivent concéder la conjugaison dans le triangle basal : par exemple 5...Rg7 ("3") 6.Rd3! ("3"), et les Blancs gagnent
D3) 4...Rf7 ("1") (ou 4...Rh7 avec une suite symétrique), s’écarte de la traverse principale, et permet donc au Roi Blanc de pénétrer dans la zone principale par une nouvelle manœuvre de contournement : 5.Rc2! ("6") sans concéder la conjugaison [sur 4...Rh7 ("7"), les Blancs auraient contourné le Roi Noir par 5.Rc4! (la case "4" étant inaccessible au Roi Noir)]
Si on poursuit cette variante (1.Ra2 Rg8 2.Ra3 Rf8 3.Rb2 Rg7 4.Rb3 Rf7 5.Rc2), les Noirs disposent maintenant des coups suivants :
D31) 5...Rf8 ("4"), le Roi Noir reste en bordure de la zone de conjugaison et ne revient pas sur une traverse principale; le Roi Blanc peut donc poursuivre sa manœuvre de contournement le long de la bordure opposée (2ème rangée) et joue donc 6.Rd2! ("7") qui lui permet de progresser dans la zone principale vers le "chemin le plus court" sans obtenir la conjugaison mais sans la concéder non plus, la case "7" (h7) n’étant pas accessible au Roi Noir.
Le Roi Blanc menaçant de pénétrer par e3-f4, le Roi Noir doit se rapprocher par 6…Rf7 ("1") (6…Rg7 ("3") concèderait directement la conjugaison au Roi Blanc dans le triangle basal avec 7.Rd3). Le Roi Blanc poursuit alors son contournement le long de la bordure (2ème rangée) par 7.Re2 ("8"), la case "8" correspondante (h6) étant inaccessible au Roi Noir.
Mais cette fois-ci le Roi noir n’a plus vraiment d’autre choix que de jouer 7…Rg7 ("3") (6…Rg6 ("2") concèderait directement la conjugaison au Roi Blanc sur le chemin le plus court par 8.Re3). Le Roi Blanc s’empare bien sûr de la conjugaison dans le triangle basal par 8.Rd3 ("3"). L’étape suivante consistera à atteindre le chemin le plus court en conservant la conjugaison par 8…Rg6 ("2") 9.Re3 (ou 8…Rf7 ("1") 9.Rd4).
Une fois obtenue la conjugaison sur le chemin le plus court, la dernière étape de la lutte pour les points de pénétration consiste simplement à se diriger à l’opposé du Roi Noir. Par exemple après 9...Rf7(g7) 10.Rf4 et les Blancs gagnent le Pion g4, ou 9...Rh6 10.Rd4 et les Blancs gagnent le Pion e6.
D32) 5...Rg8 ("5") (ou 5...Rg7 ("3")), le Roi Noir regagne une traverse principale de la zone de conjugaison (colonne g) et le Roi Blanc peut prendre la conjugaison sur la traverse correspondante (3ème rangée) par 6.Rc3 ("5") (ou 6.Rd3 ("3")). Le Roi Noir peut alors retarder la pénétration du Roi Blanc sur le chemin le plus court mais il ne peut l’empêcher indéfiniment : par exemple 6...Rf8 ("4") 7.Rc4 ("4") Rf7 ("1") 8.Rd4 ("1"). Les Blancs ont maintenant la conjugaison sur le chemin le plus court et ils procèdent ensuite comme dans la variante précédente (D31) ; par exemple 8...Rf8 9.Re3 et les Blancs gagnent le Pion g4.
D33) 5...Rg6 ("2"), le Roi Noir regagne une traverse principale de la zone de conjugaison mais la case conjuguée (case e3) n’est pas accessible au Roi Blanc. Par 6.Rc3 ("5"), le Roi Blanc peut tout de même progresser sur la traverse correspondante en allant lui aussi sur une case dont la conjuguée (case g8) n’est pas accessible au Roi Noir. Celui-ci devant empêcher la pénétration du Roi Blanc par c5-d6, il ne dispose guère mieux que du coup 6...Rg7 ("3"), après quoi le Roi Blanc récupère la conjugaison sur la case centrale avec 7.Rd3 ("3"), et on se retrouve dans une situation déjà vu plus haut (voir D31).
Voilà, j’espère ne pas avoir commis trop d’erreurs. L’exposé est sans doute trop long et trop détaillé, mais si Tantale (au moins lui) est aussi motivé qu’il en a l’air, ce post consacré à un cas de système de conjugaison à 8 cases pourrait lui être profitable en complément de mon ancien post sur le système du triangle-carré.
J’ai repris ici la même trame en insistant beaucoup plus sur la manœuvre de contournement qui me semble une étape essentielle et souvent mal expliquée et/ou mal comprise.
|
|
|
Superbe exposé.
Je reproduis ici le petit dessin que j'ai tracé au fur et à mesure de la lecture de cet article.
|
|
|
Mille mercis à Kloch pour tout ce travail et cette grande clarté dans les explications (même si je n'ai pas encore tout lu).
Mais par contre je me demande si ce n'est pas un peu ardu en partie de retenir toutes les cases conjuguées car bien sûr on a pas le droit de noter quoi que ce soit.
Est-ce que certains ici peuvent pratiquer cette théorie des cases conjuguées en partie et n'est ce pas trop difficile de tout retenir? Ont-ils des astuces que j'ignorerais ?
|
|
|
Très bien expliqué!
|
|
|
Afin de pouvoir encore mieux suivre, j'ai reproduit les coups indiqués par Kloch dans cette partie - Solution de Kloch .
(Utiliser Internet Explorer)
Les Blancs jouent et gagnent.

|
|
|
Je crois que Tantale et moi avons oublié de mentionner l’auteur de l’étude : Bianchetti (1925).
Je viens de tomber sur une étude de Chupin (1982) qui reprend la même structure de pions avec couleurs inversées :

les Blancs jouent et annulent.
La solution (1.Ra1! Rh6 2.Rb1! etc =) est bien sûr évidente si on a compris l’étude de Bianchetti.
|
|
|
Tantale ta aimé l'anti-opposition ? :)
|
|
|
J'ai ajouté la solution de l'étude de Emmanuel Lasker & Gustavus Charles Reichhelm -1901 - qui avait été analysée par Kloch ici sur France-échecs le 31/07/2007 à 02:49:38.
Je vais maintenant faire une petite pause avec les cases conjuguées sinon je vais finir par en voir sur le carrelage de ma salle de bain.
@Bibifoc: C'est quoi l'anti-opposition? C'est le conformisme?
Les Blancs jouent et gagnent.

|
|
|
Je viens de recevoir cet email:
This study [attributed by Averbakh and Maizelis to Bianchetti,
1925] takes me back a bit. Many years ago, I wrote a program to solve
K&P endings, esp blocked ones, by constructing graphs corresponding to
the [less than] 4096 king positions for each pawn formation and
searching the graphs. This was much faster than the usual depth-first
search techniques, esp in drawn positions [where the search could
easily go to a full 100 ply before either the 50-move rule or a
repetition occurred], as there was no backtracking, and indeed no
analysis tree. [It takes 27 ply, which even today is not entirely
trivial, to establish the win of a pawn in the Bianchetti study.]
The program could solve all the "corresponding squares" studies
in A&M and in Cheron, usually in a few seconds [corresponding to a few
milliseconds on a modern PC]. Sadly, it was pretty useless for K&P
endings with mobile pawns, and absolutely useless for anything else.
Kloch's analysis of the Bianchetti study is very clear. This
is a topic which most books or chapters on K&P endings treat rather
badly, serving to obscure rather than illuminate the principles.
--
Andy Walker,
|
|
|
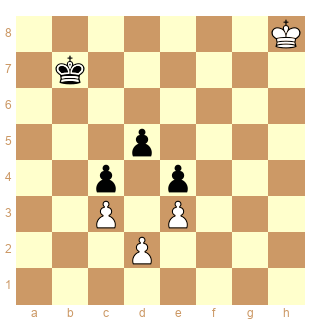
Une autre étude de Rinaldo Bianchetti - 1926 - Les Blancs jouent et gagnent.
1.Rh7! Rb6 2.Rh6! Rb5 3.Rg7! Rc6 4.Rg6! Rc7 5.Rf5! Rd7 6.Re5! Rc6 7.Re6! Rc5 8.Rd7! 1-0
Je pense qu'avec les cases conjuguées c'est assez facile à trouver. Je verrai cela demain.
|
|
|
hé bien! cette guirlande va passer dans mes favoris !!
par ailleurs , après le mot ( mail) de Tantale j'ai trouvé ceci qui ne me parait pas hors sujet :
•Andrew N. Walker (1989). Interactive Solution of King and Pawn Endings.
seconde puce du paragraphe : Selected Publications
|
|
|
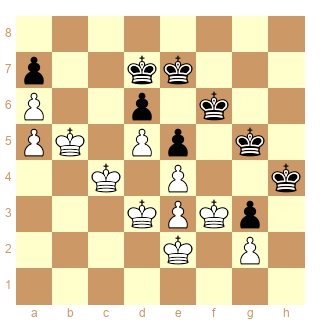
Voici une autre position avec pions bloqués (Ebersz 1930) qui n’est pas sans rappeler celle de Bianchetti.

|
|
|
Les Blancs ont à nouveau 2 points de pénétration (c6 pour gagner le Pion Noir d6 et f3 pour gagner le Pion Noir g3) contre aucun pour les Noirs, et le traitement de cette position sera similaire à celui exposé plus haut pour l’étude de Bianchetti.
En résumé,
1. zugzwangs réciproques : b5/d7 et f3/h4
2. chemin le plus court : (b5)-c4-d3-e2-(f3) vs (d7)-e7-f6-g5-(h4)
|
|
|
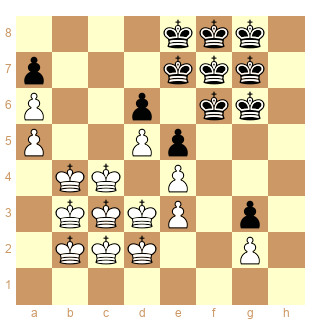
Nous avons vu que le système de conjugaison à 8 cases est une extension du système triangle-carré. Ici la particularité de cette position réside dans le fait qu’on peut identifier 2 systèmes de conjugaison à 8 cases en utilisant chacune des paires de cases du chemin le plus court pour former le triangle basal.
Premier système de conjugaison à 8 cases en utilisant les cases c4-d3/e7-f6 :
|
|
|
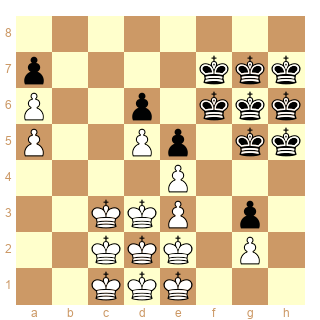
Second système de conjugaison à 8 cases en utilisant les cases d3-e2/f6-g5 :
|
|
|
On peut bien sûr se contenter d’utiliser l’un ou l’autre de ces systèmes pour résoudre l’étude (comme le fait Maizelis).
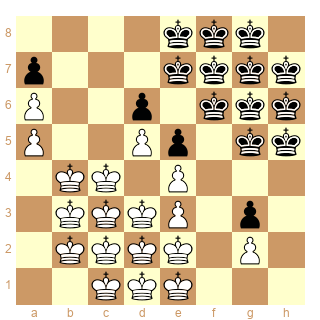
Une autre façon de procéder (qui n’est pas forcément plus simple en pratique mais qui est sans doute plus rigoureuse dans son application et plus générale dans sa portée) consiste à étendre autant que possible la zone de conjugaison principale (comme le font Halberstadt et Averbakh/Zinar). Il suffit ainsi de fusionner ces 2 systèmes à 8 cases en un seul pour former une zone à 12 cases :
|
|
|
Je rappelle que les zones de conjugaison principales correspondent à l’ensemble des cases conjuguées non ambiguës retrouvées dans les deux camps et présentant une structure et des propriétés géométriques identiques.
Dans l’étude de Bianchetti, seule la zone à 8 cases des Blancs pouvait être étendue pour former de ce fait une zone secondaire.
Dans l’étude d’Ebersz, on peut encore étendre dans les 2 camps et de façon similaire les zones à 8 cases (ou la zone fusionnée à 12 cases) jusqu’à former un carré 4x4 tronqué. En effet, les zones précédentes à 12 cases peuvent de façon évidente être encore complétées dans les 2 camps, respectivement par les cases b1 et h8 pour former finalement une zone de conjugaison principale à 13 cases.
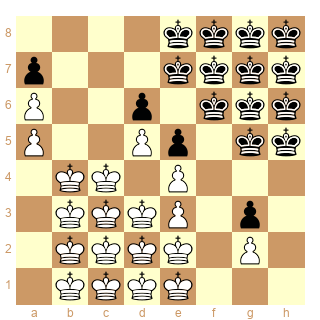
On peut ainsi proposer la numérotation suivante (en commençant par les cases du chemin le plus court) :
1 = c4 / e7
2 = d3 / f6
3 = e2 / g5
4 = c3 / f7
5 = d2 / g6
6 = c2 / g7
7 = b4 / e8
8 = b3 / f8
9 = b2 / g8
10 = b1 / h8
11 = c1 / h7
12 = d1 / h6
13 = e1 / h5
Dans la camp des Blancs uniquement, on peut étendre cette zone sur la colonne a pour former une zone secondaire :
case a4 = 1a
case a3 = 4a
case a2 = 6a
case a1 = 11a
|
|
|
Le Roi Noir étant en h8 ("10"), la solution est donc 1.Rb1!
La progression se fera ensuite en direction du chemin le plus court (cases 1-2-3) que le Roi Blanc devra atteindre avec la conjugaison (sauf bien sûr si le Roi Noir se laisse distancer avant). Par ordre d’intérêt, le Roi Blanc visera ensuite de préference les cases contiguës formant les triangles basaux (cases 4-5).
Les manœuvres de contournement pourront ici s’opérer autour de 2x2 traverses principales.
En effet les zones de conjugaison (carrés 4x4 tronqués) comportent 2x2 lignes médianes (à la différence du carré 3x3 tronqué du système à 8 cases qui comporte une seule ligne médiane horizontale et une seule ligne médiane verticale) :
- 2ème et 3ème rangées pour les Blancs vs colonnes g et f pour les Noirs
- colonnes c et d pour les Blancs vs 7ème et 6ème rangées pour les Noirs
Une suite possible pourrait être :
1.Rb1! ("10" = conjugaison)
1...Rh7 ("11")
2.Rc1! ("11" = progression avec conjugaison; les Rois ont atteint une traverse médiane : colonne c vs 7ème rangée)
2...Rh6 ("12", le Roi Noir quitte la traverse médiane)
Dans cette position, les Blancs peuvent déjà opérer une manœuvre de contournement :
A) 3.Rb2(!) ("9" = progression par contournement)
Le Roi Blanc menace de pénétrer par b5-c6, ce qui contraint le Roi Noir à le suivre à distance en gagnant la colonne g :
A1) soit par 3...Rg7 ("6")
4.Rc2! ("6", progression avec conjugaison) et le Roi Noir n’a guère mieux que de laisser les Blancs prendre la conjugaison sur un des sommets des triangles basaux, puis sur le chemin le plus court.
Par exemple:
4...Rg6 ("5", triangle basal)
5.Rd2! ("5", progression avec conjugaison sur un triangle basal)
5...Rf6 ("2", chemin le plus court)
6.Rd3! ("2", progression avec conjugaison sur le chemin le plus court)
et au coup suivant le Roi Noir devra se laisser distancer par le Roi Noir, d’un côté ou de l’autre.
A2) soit par 3...Rg5 ("3")
4.Rc3(!) ("4", progression par contournement, car le Roi Blanc ne peut pas récupérer la conjugaison mais il peut progresser vers b5-c6 sans la concéder. 4.Rc3 est plus précis que 4.Rb3 car il rapproche le Roi Blanc à la fois de c5-d6 et du chemin le plus court, ce qui accélère le gain)
Pour ne pas se laisser distancer, le Roi Noir doit maintenant jouer 4...Rf6 ("2", chemin le plus court)
5.Rd3! ("2", progression avec conjugaison sur le chemin le plus court)
et l’issue est la même que précédemment
A3) soit par 3...Rg6 ("5", triangle basal)
4.Rb3! ("8", progression par contournement, car le Roi Blanc ne peut pas récupérer la conjugaison mais il peut progresser vers b5-c6 sans la concéder. C’est ici l’unique coup gagnant)
Pour ne pas se laisser distancer, le Roi Noir doit maintenant jouer sur la colonne f, mais contrairement à la variante A2, il a ici le choix entre :
- 4...Rf7 ("4", triangle basal)
5.Rc3! ("4", progression avec conjugaison sur un triangle basal)
5...Rf6 ("2", chemin le plus court)
6.Rd3! ("2", progression avec conjugaison sur le chemin le plus court)
et l’issue est la même qu’en A1
- 4...Rf6 ("2", chemin le plus court)
5.Rb4! ("7", progression par contournement, car le Roi Blanc ne peut pas récupérer la conjugaison mais il peut progresser vers b5-c6 sans la concéder)
Pour ne pas se laisser distancer, le Roi Noir doit maintenant jouer 5...Re7 ("1", chemin le plus court)
6.Rc4! ("1", progression avec conjugaison sur le chemin le plus court)
et l’issue est la même que précédemment
Après 1.Rb1! Rh7 2.Rc1! Rh6 les Blancs peuvent aussi poursuivre par :
B) 3.Rd1 qui maintient la conjugaison sur un autre couple de traverses médianes (colonne d vs 6ème rangée).
C’est la suite donnée par van der Heijden (Study database) et Averbakh/Zinar (Comprehensive Chess Endings).
Elle est tout aussi valable que le contournement. En effet progresser avec la conjugaison sur un deuxième couple de traverses médianes plus "interne" semble limiter l’arbre de variantes plausibles, mais a priori sans raccourcir ces variantes. D’un autre côté on peut préférer d’un point de vue pratique s’astreindre à procéder au contournement dès que l’occasion se présente sans la différer.
D’ailleurs Zinar se "rattrape" au coup suivant par 3...Rh5 ("13") 4.Rc2! ("6", contournement) 4...Rg6 ("5") 5.Rd2! ("5", conjugaison sur un triangle basal) 5...Rf6 ("2") 6.Rd3! ("2", conjugaison sur le chemin le plus court qui assure un gain rapide).
En revanche la suite donnée par van der Heijden ne me paraît pas du tout convaincante :
3...Rh5 ("13")
4.Re1(?!) ("13", s’entête à conserver la conjugaison en bordure de la zone de conjugaison, ce qui ne présente maintenant aucun intérêt)
4...Rg6 (?!) ("5", facilite la tâche des Blancs, alors qu’en reculant par 4...Rh6!?, les Noirs auraient contraint le Roi Blanc à reconnaître son erreur et à faire de même par 5.Rd1!, seul coup alors pour rectifier le tir et sauver le gain)
La suite retombe finalement sur la variante de Zinar :
5.Rd2! Rf6 6.Rd3!
Mais ici van der Heijden ajoute :
6...Re7 7.Rc4(?!) Rd7 8.Rb5(?!) +-
ce qui semble à nouveau perdre des temps (j’en compte quatre) car après 8...Rc7, le Roi Blanc doit repartir dans l’autre sens (9.Rc4) pour gagner le Pion g3, alors qu’il pouvait le faire dès le 7ème coup par 7.Re2(!), et même encore au 8ème coup par 8.Rd3(!) puisqu’il avait à chaque fois la conjugaison sur le chemin le plus court.
Concernant les travaux d’Andy Walker, cela semble rejoindre ce que je disais sur l’utilisation des graphes pour résoudre les finales de Pions avec pions bloqués (30/08/2012 - 00:22:14).
Je pensais avoir été un peu original en la matière car la puissance de calcul des machines actuelles ne nécessite pas une telle approche, et j’étais loin d’imaginer qu’à la préhistoire des programmes d’échecs quelqu’un ce soit intéressé spécifiquement à ce type de positions.
|
|
|
Ebersz a utilisé la même structure de Pions que dans l’étude précédente avec couleurs inversées pour aboutir à une étude dont la solution peut sembler encore plus contre-intuitive :

Les Blancs jouent et annulent
Solution : 1.Rb2!! Rg8 2.Ra1!! =
|
|
|
Toujours afin de mieux suivre la démonstration de Kloch j'ai ajouté sa solution de l'étude de Karel Ebertz 1930 à la page Cases conjuguées
Les Blancs jouent et gagnent
On attend l'analyse de l'étude de Karel Ebersz 1930 du 03/09/2012 - 02:13:13 !

|
|
|
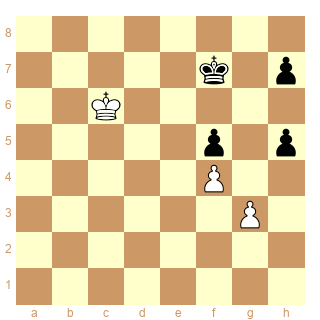
Une position intéressante issue d'un livre de Robert Fine (1941)
Les Blancs jouent et gagnent.
Analyse ici
(utiliser Internet Explorer)
Les ordinateurs rament très longtemps.

On arrive à la position (trait aux Blancs) dans laquelle interviennent les cases conjuguées.
|
|
|
Correction, c'est Reuben Fine et non Robert Fine.
|
|
|

A priori cette 2ème étude d'Ebersz que j'ai postée ne nécessite pas vraiment de commentaires supplémentaires puisque la structure de pions est strictement identique à celle de la 1ère étude (post du 03/09/2012 - 01:56:58). La position est juste inversée pour se placer du point de vue de la défense.
Les Blancs au trait jouent et annulent en s'emparant de la conjugaison dans la zone principale et en ne la lâchant plus du fait de la structure des zones de conjugaison (zones secondaires puisque les zones principales sont par définition comparables) qui ne permet aucune manœuvre particulière pour les Noirs (par exemple pas de dégénérescence ou autre particularité géométrique leur permettant de perdre un temps).
D'où la solution que j'ai donnée.
En effet, si on reporte la même numérotation des cases conjuguées :
1 = d2 / f5 (h5)
2 = c3 / e6
3 = b4 / d7
4 = c2 / f6 (h6)
5 = b3 / e7
6 = b2 / f7 (h7)
7 = d1 / g5
8 = c1 / g6
9 = b1 / g7
10 = a1 / g8
11 = a2 / f8 (h8)
12 = a3 / e8
13 = a4 / d8
le Roi Noir en h7 se trouve sur une case "6a") :
1.Rb2!! ("6" = conjugaison)
1...Rg8 ("10" juste pour voir si les Blancs suivent)
2.Ra1!! ("10" on dirait que oui)
etc
En revanche il serait peut-être plus utile d’ajouter un commentaire sur l’étude de Bianchetti 1926 (Tantale, le 02/09/2012 - 21:23:32).
J’y reviendrai à une autre occasion.
|
|
|
J'ai rajouté à la page des cases conjuguées la deuxième étude de Karel Ebersz 1930.
Les Blancs jouent et annulent.

|
|
|
J'aime beaucoup le graphisme des tableaux pour illustrer les positions.
Sur un plan historique : Grigoriev a choisi son étude, parmi quelques autres, pour présenter les cases conjuguées en 1922.
Une petite rectification sur le tableau :
- f6 est conjuguée avec f4 et h3 (cases 1)
- g6 est conjuguée avec h4 et f3 (cases 2)
- g7 est conjuguée avec g3 (cases 3)
Comme la case f7 est interdite au Roi noir, la solution devrait apparaître clairement sur le plan graphique. Le triangle g7-g6-f6, dont dispose le Roi noir, se retrouve un peu aplati chez les Blancs (f3-g3-h3) et il leur suffit d'amener leur Roi en g2 pour gagner.
|
|
|
Merci Slucaino
Je rectifie le graphique.
|
|
|
J'ai acquis le livre « Endgame Magic » de John Beasley & Timothy Whitworth d'occasion (on ne le trouve plus neuf je crois), un livre magique.
On y trouve un exemple de cases conjuguées dans une position avec un Fou et un Cavalier (étude d'Artur Mandler 1924).
Un raisonnement conduit à attribuer à chaque case que le cavalier peut occuper la case correspondante que le fou doit aller occuper pour maintenir la nulle.
Diagramme

|
|
|
Tantale attention tu vas plus pouvoir rentrer dans ta salle de bains :)
Sinon ta 2 liens qui je crois non pas été cité dans archives chesscafe dans Endgame Corner.Fevrier et mars 2004 : The Mystical sisters squares.
|
|
|
D'autres exemples de cases conjuguees du Dvorestky
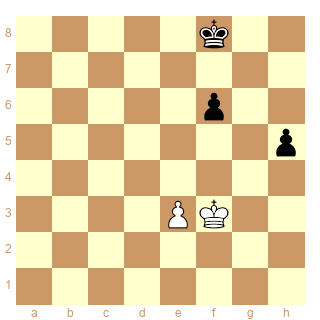
Gulko-Short Riga 1995

Reti,1929 blancs jouent et nulle
|
|
|
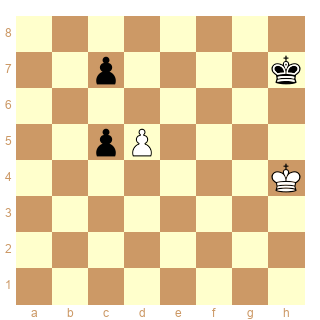
M.Zinar 1987 Blancs jouent et nulle
|
|
|
@Bibifoc pas grave je ne me laverai pas.
|
|
|
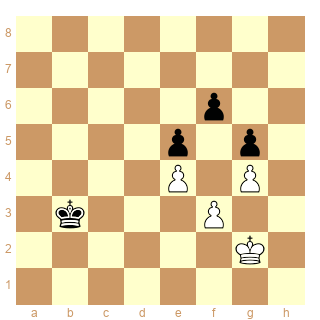
Un cas d'anti-opposition résolu par les cases conjuguées.
Les Blancs jouent et font nulle.
diagramme
|
|
|
Pour cet exemple tiré d'une partie Gulko-Short 1995 Dvoretsky ne donne pas les cases conjuguées.
J'ai essayé de les établir. Est-ce correct? (Peut-être Slucaino ou qq d'autre peut me répondre).
Bien que les pions ne soient pas bloqués, je crois qu'on peut parler de cases conjuguées.
Diagramme
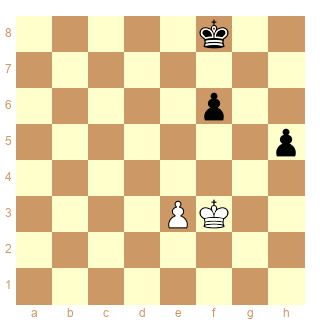
|
|
|
Pour cet exemple tiré d'une partie Gulko-Short 1995 Dvoretsky ne donne pas les cases conjuguées.
J'ai essayé de les établir. Est-ce correct? (Peut-être Slucaino ou qq d'autre peut me répondre).
Bien que les pions ne soient pas bloqués, je crois qu'on peut parler de cases conjuguées.
|
|
|
Je ne suis pas arriver à modifier le post ci-dessus. Bug?
|
|
|
Pour cet exemple tiré d'une partie Gulko-Short 1995 Dvoretsky ne donne pas les cases conjuguées.
J'ai essayé de les établir. Est-ce correct? (Peut-être Slucaino ou qq d'autre peut me répondre).
Bien que les pions ne soient pas bloqués, je crois qu'on peut parler de cases conjuguées.
|
|
|
Diagramme
|
|
|
Diagramme
|
|
|
Diagramme
|
|
|
. Diagramme
|
|
|
Test
|
|
|
Diagramme
|
|
|
diagramme
|
|
|
Test
|
|
|
Ca parait correct mais je ne suis pas assez fort pour le confirmer :)
ps : tu as deja illustré avec Paul Delvaux ?
ps2 : ta des carreaux dans tes WC ? :)
|
|
|
ça parait correct tes cases mais je suis dans l'incapacité totale de confirmer vu mon faible niveau :)
ps : Tu as déja illustré avec Paul Delvaux ?
ps2 : tu as des carreaux dans tes WC ?
|
|
|
Y'a un problème dans le fil des Olympiades non?
|
|
|
opps desole pour le doublon lag du site
|
|
|
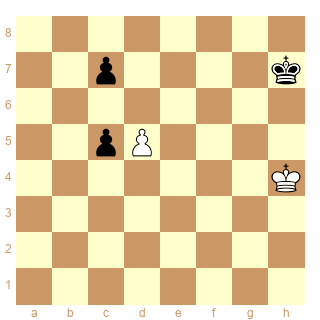
Pour l'étude de Mikhail Afanasievich Zinar - 1980
proposée par Bibifoc j'ai dressé la table des cases conjuguées.
Diagramme
|
|
|
Cette étude de Charles Dealtry Locock - 1892 se résout également avec les cases conjuguées.
Solution

|
|
|
Cet exemple a été traité dans « L'opposition et cases conjuguées sont réconciliées », par Vitaly Halberstadt and Marcel Duchamp.
Extraits originaux de ce texte
|
|
|
F.Dedrle (1921) noirs jouent et nulle
|
|
|
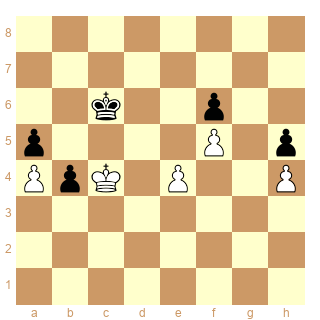
Pour la partie Seirawan - Kasparov 1983
j'ai établi les cases correspondantes en suivant les explications de Slucaino.
J'espère que c'est juste.
Diagramme
|
|
|
Cette étude, les Blancs jouent et font nulle peut certainement aussi se résoudre par les cases conjuguées.
Si quelqu'un veut s'y lancer.
Walter Bähr - (=0000.56g4b8)
2.hm Tijdschrift v.d. KNSB#228 (tw), 1938
1.Rh4 Rb7 2.Rg4 Rc8 3.Rg3 Rc7 4.Rh3 Rd8 5.Rg4 Re8 6.Rh5 Re7 7.Rg5 Rd7 8.Rh4 Rd6 9.Rg4 Rc5 10.Rf3 Rc6 11.Rg3 b5 12.Rf2 Rb6 13.Rf1 Ra6 14.Rf2 Ra7 15.Rg2 Ra8 16.Rh2 Rb8 17.Rh1 Rb7 18.Rg1 Rc7 19.Rg2 Rc8 20.Rh2 Rd8 21.Rh3 Re7 22.Rg4 Rf6 23.Rh5 Re7 24.Rg4 Rd7 25.Rg3 Rd6 26.Rf3 Rc5 27.Re3 b4 28.cxb4+ Rxb4 29.Rd2 ½-½

|
|
|
Un peu de vigilance, Tantale, si les cases sont indiquées sur mes indications (et même sinon) ! f3 et f4 ne font pas parties des cases conjuguées et les autres devraient l'être un peu différemment.
Je remets les explications postées plus haut :
Un coup plus tôt, le Roi noir se trouvait en c5 et le blanc en d3, sa seule case. Les cases c5 et d3 sont conjuguées.
Les cases d6 et d4 sont conjuguées aussi.
La case c6 et conjuguée avec c4 ou e3.
Lorsque le Roi noir se trouve en d7 ou c7, il menace d'aller en c6 ou d6 et le Roi blanc ne doit se trouver ni en c4, ni en d4, ni en e3 mais être prêt à s'y rendre, c'est-à-dire qu'il doit être en d3. Le Roi noir n'a qu'à attendre un coup entre c7 et d7 pour que les Blancs se trouvent en Zugzwang. Tout cela se voit bien dans le déroulement de la partie.
|
|
|
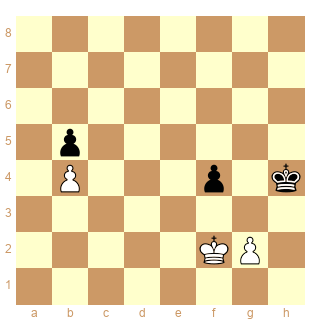
Cette étude (1924) de Henri Gerard Maria Weenink (1892 - 1931) peut-elle être résolue par les cases correspondantes.
Il semble que les cases h4/f3 g5/e4 f5/d5 "correspondent" c'est à dire que quand le Roi noir est en h4 si le Roi blanc peut aller en f3 il gagne, etc.
1.Rf3! Rg5 2.Re4! Rg4 3.Rd5 Rh5 4.Rc5 Rg5 5.Rc6 Rf5 6.Rd5! Rf6 7.Re4 Rg5 8.Re5 Rg4 9.Rf6 Rh4 10.Rf5 Rg3 11.Rg5 1-0
|
|
|
Merci Slucaino.
J'ai corrigé le graphique et je me suis permis de faire un copier-coller de tes explications en dessous du graphique.
Montaigne disait « Mieux vaut une tête bien faite qu'une tête bien pleine »
J'ai l'impression que j'ai ni l'une ni l'autre.
|
|
|
que je n'ai*
|
|
|
Pour l'étude (1924) de Henri Gerard Maria Weenink (1892 - 1931) j'ai découvert après le post ci-dessus qu'elle était traité Dvoretsky's Endgame Manual, 2nd ed., à la position 1 - 15, Exercise 1/2 au chapitre traitant des cases correspondantes (opposition).
En fait le Roi blanc doit gagner l'opposition et pour cela aller menacer (sans le prendre) le pion le pion b5 (c'est le seul moyen)
J'ai ajouté cette étude à la page des cases conjuguées bien qu'il ne s'agisse que d'opposition.

|
|
|
On voit dans cette étude que la menace est plus forte que l'exécution.
On gagne en menaçant de gagner le pion b5 mais on ne le prend pas.
On gagne donc en faisant peur aux noirs.
|
|
|
Un lien utile semble avoir été oublié. Je tentais d'initier des promeneurs initialement réfractaires. Malgré le sabotage des diagrammes, on doit pouvoir le lire. Je suppose que vous êtes équipés, donc la notation Forsythe ("fen") vous donne le diagramme instantanément, par exemple dans la case "coller FEN" de "chess bouse".
Concernant l'étude de Bianchetti, il me semble qu'il y a deux variantes d'égale longueur qui en soulignent la richesse :
3...Rf7 4.Rc2! Rf8 5.Rd2! Rf7 6.Re2! Rg7 7.Rd3! Rg6 8.Re3! Rh6 9.Rd4!
3...Rg7 4.Rb3! [4...Rf7 5.Rb4! Re8 6.Rc3! Re7 7.Rd3! Rf7 8.Rd4!] Rg8 5.Rc3! Rf8 6.Rc4! Re8 7.Rd3! Rf7 8.Rd4! Re7 9.Re3! .
Gulko-Short fut brièvement commentée dans LSF3 le 16/10/2010 à 14:29. Elle mériterait un exposé complet, que j'aurai plaisir à rédiger quand le public féiste manifestera au travail une assiduité digne d'une troisièmenationéchiquéennedumondesic.
Je ne sais pas ce qu'en dit Zinar, le grand-maître des finales de pions, mais Halberstadt et Chéron avaient déjà classé les différents cas de cases conjuguées, en donnant à chacun un chiffre et une lettre. Ayant constaté que les complexes de cases blanches et noires (un peu éloignées des cases de contact immédiat) se déduisaient toujours l'un de l'autre par une symétrie d'axe horizontal ou diagonal, éventuellement composée avec une translation horizontale, ils donnaient la longueur (en nombre de cases) de la translation, suivie de la lettre H ou D selon la nature de la symétrie.
Ainsi, l'étude de Locock (le premier exemple de l'article, étrangement délaissé) appartient à la catégorie 0D : pas de translation, une simple symétrie, les cases c2, d2 et e2, par exemple, étant symétriques de leurs conjuguées respectives h7, h6 et h5 par rapport à la diagonale h2-b8.
L'étude de Bianchetti détaillée par Kloch appartient à la catégorie 1D. Considérez en effet les mêmes cases (c2, d2 et e2) et leurs conjuguées respectives h8, h7 et h6. On passe des premières aux secondes en les poussant d'une case vers la gauche ou, si l'on veut faire chic, en leur appliquant une translation de vecteur (-1,0), soit b2, c2, d2 puis en faisant une symétrie, également par rapport à la diagonale h2-b8.
De même celle d'Ebersz. Poussez e8, f8 et g8 d'une case vers la droite, translation de vecteur (1,0), vous obtenez f8, g8 et h8 ; symétrisez par rapport à la grande diagonale blanche a8-h1, vous tombez sur... leurs conjuguées a3, a2 et a1.
L'étude de Lasker/Reichhelm appartient à la catégorie 1H. Voyez les cases b2, c2 et d2. Leurs conjuguées respectives sont a8, b8 et c8. On a fait le déplacement d'une case vers la gauche, puis une symétrie, d'axe cette fois horizontal, par rapport à la 5e rangée. De même une étude de Bähr (Rc1/Rc7).
Le cas 2D est illustré par une étude d'Halberstadt avec PBa4 et b5, le cas 3D est illustré par une autre de Bianchetti (avec PBa6). Je n'ai pas vérifié d'autres cas mais si le coeur vous en dit...
|
|
|
Le lien utile a été corrigé.
|
|
|
l'étude de Locock a été traitée 06/09/2012 - 10:05:34
|
|
|
Locock : cela ne m'avait pas échappé. Mais un diagramme d'en-tête d'un article mérite un meilleur traitement qu'un lien. C'est du moins ma conception. Sans aller jusqu'à le traiter klochement, la solution aurait pu (dû) figurer quelques centimètres au-dessous.
Mille fois merci Modo 2. Mais, vous le savez, je suis un adepte de la devise "on n'a rien donné quand on n'a pas tout donné" c'est-à-dire, en langage clair, un enquiquineur. Les trois articles LSF pourraient-ils être également corrigés ? Je veux bien faire le travail moi-même si vous me donnez la main (j'ignore si c'est possible) et... si c'est à ma portée.
Pour une meilleure lecture du lien utile obligeamment rafraîchi par Modo 2, je me permets de remettre les plus importants des titres ayant sauté en 2011.
Les cases conjuguées, expliquées pour les nuls était le titre donné le 20-08-2009 à 13:39. L'explication détraumatisante suit immédiatement.
Considérez à présent cette position le 23-08-2009 à 18:15
Les cases f5 et e8 sont conjuguées. Posez maintenant le Roi blanc en e4 à 18:18
Toujours avec le RB en e4 à 18:24
Voyez maintenant ce diagramme à 18:46
Avez-vous bien suivi ? à 18:55
Ce sera encore plus clair. Bonne lecture.
Je ne sais pourquoi je pense à la phrase de Lyautey après dévastation de magnifiques arbres, répondant à ceux qui rechignent à replanter, se plaignant qu'il faudra un siècle pour les voir repousser : "C'est une bonne raison pour commencer tout de suite". Et je ne sais pas non plus pourquoi (mais l'esprit a de ces raccourcis...) je me vois, ou plutôt mes arrière-petits-enfants, à l'Olympiade 2112...
|
|
|
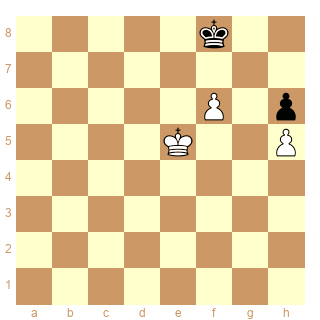
Pour l'éude de Les Blancs gagnent (Karel Ebersz, 1935) de ce fil
que faut-il corriger à ce diagramme pour qu'il soit correct?

|
|
|
Me paraît correct. Et me fait penser que j'avais oublié de mentionner l'essai 1 Rf2? Rd7! (je l'ai seulement inclus dans 1 Re2?). On peut aussi ajouter un "7" sur la case d3. Notons que la classification ci-dessus ne mène pas à grand-chose ici (ce serait apparemment 2D puisque e3-f3 devient c7-c8), les accidents de l'échiquier (case f7 indisponible) empêchant que deux trios de cases horizontales ou verticales se correspondent, ce qui vient de ce que f7 est en quelque sorte remplacée par d8 et donc le système est "tordu".
Notez que dans le classique (prétendument Fahrni-Alapin, 1912) où un auteur batave écrivait que "les Blancs ne progressent plus" alors qu'ils gagnent en 4 coups, nous sommes apparemment aussi dans 2D puisque e5-f5 devient f8-f7, mais il serait meilleur de parler de cases semi-conjuguées car il est possible de trianguler. En outre il n'y a pas de cases conjuguées éloignées, comme le souhaitaient VH & AC.
5k2/8/5P1p/4K2P/8/8/8/8
|
|
|
Je viens donc de rajouter l'étude de Kornel Ebersz 1935 avec un lien sur les explications d'Erony de France-échecs à la page des cases conjuguées.
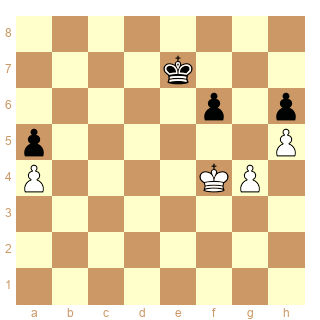
J'ai aussi saisi l'exemple trouvé dans ChessCafé 39 (Merci Bibifoc) expliqué par Karsten Müller.
Diagramme : les Blancs jouent et gagnent.
|
|
|
Juste deux remarques concernant Gulko-Short.
Cette finale exceptionnelle, où l'analyste ne peut qu'admirer la défense blanche, d'une haute précision, commence au 46e coup. Il faut savoir qu'après avoir dû monter jusqu'en f5, le Roi blanc fut contraint de redescendre, au moyen de quatre coups uniques (car il avait dû remonter), 47 Rf4!!, 48 Rg3!!, 50 Rf3!! et celui que vous signalez, 51.Rg2!!.
La fin de la partie n'est pas celle que vous indiquez. Vous êtes parfaitement en droit de choisir autre chose en variante principale. Moi-même, je ne m'en prive pas. Mais je vous conseille alors de le préciser. Dans le cas présent toutefois, malgré le dual 52 Rf2! ou 52 Rf3!, je trouve la fin de la partie plus intéressante et vous la livre sans commentaire :
51... Rg8 52.Rf2 Rf8 53.Rg2 Re7 54.Rh3 Rf7 55.Rg3 Rg6 56.Rf4 Rh6 57.Rf5 Rh7 58.e4 Rh6 59.Rxf6 h4 ½–½
|
|
|
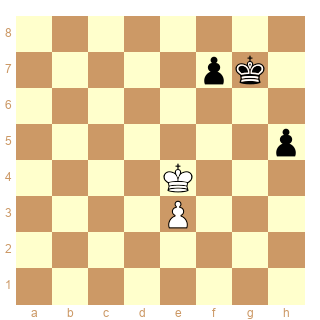
Je vous donne le diagramme de départ à titre d'information.
(Gulko-Short 1995 après le 45e coup noir)
8/5pk1/8/7p/4K3/4P3/8/8
|
|
|
Je rajoute la partie.
|
|
|
L'étude "du livre de Fine", en réalité analysée par Hooper & Maizelis après 1958, est démolie, as usual, puisque la suite que vous donnez sur 1 Rd4 mène, après 6 h5! gxh5 7 e6 Rc6 8 Rxa6, à la même position que la variante principale.
|
|
|
Elle est démolie en tant qu'étude mais l'essentiel est que les Blancs gagnent et la partie intéressante est la fin qui concerne les cases conjuguées.
Je corrige la couleur de la variante 1.Rd4
|
|
|
Pas de chance. L'oeuvre de Grigoriev est prodigieuse, mais vous réussissez, comme je ne sais plus quel auteur, à dénicher une de ses rares oeuvres qui prenne l'eau de toutes parts. Cette étude de 1922 a été améliorée en 1936 par Halberstadt, bien que quelques duals subsistent.
Pour répondre à votre question, la descente sur la seconde rangée est nécessaire, mais pas nécessairement par g2. Le Roi blanc peut également passer par e2.
|
|
|
Ce que vous présentez comme "chess café 2004" est donné par VdH comme une étude de Buijs & Hendriks 1993, soit 11 ans plus tôt, juste amputée de son premier coup pour cause de dual.
Je vois que l'Allemand prend des habitudes "anglaises" (private joke).
|
|
|
L'auteur est sans doute Dvoretsky puisque je me suis borné à recopier ce passage de son livre Endgame manual.
|
|
|
L'autre exemple de "chess café 2004" ne vaut guère mieux. C'est une présentation simplement plus lourde de H. Neustadtl... 1890 !! Qui plus est, amputée de sa clef spectaculaire.
Où voyez-vous une "anti-opposition" ? Il s'agit d'un cas typique d'opposition éloignée, le nombre de cases entre les deux Rois étant impair.
|
|
|
Dvo, de son propre aveu, se moque des duals. Car il ne se soucie que de l'utilité pour les joueurs. Mais vous, passionné d'études ?
|
|
|
Je remplace "anti-opposition" par "opposition éloignée" dans le texte
|
|
|
Moi je suis pragmatique et résigné.
|
|
|
je cite Dvorestky dans le manuel des finales :
"S'il convient au contraire de céder l'opposition à l'adversaire, on est en présence d'une situation de cases conjuguées que j'appelle "anti-opposition". Ce terme me parait plus précis que l'expression "opposition de cavalier" qu'on rencontre parfois (car le mot "opposition" sous-entend un face à face des rois sur la même ligne, et non sur des lignes différentes.)"
|
|
|
Bon, je vous ai assez engueulé. Pour finir, je vous offre cette citation de Mandler, à propos du duel Fou / Cavalier. C'est lui (mais oui) qui parlait d'école élémentaire :
"Le non-initié pourrait penser que la compréhension de cette étude exige une haute expertise mathématique, alors qu'en vérité rien de plus n'est demandé que le savoir acquis à l'école élémentaire" (AM).
Laku noć.
|
|
|
@Bibifoc
En l'occurrence comme l'a dit erony, il convenait au Roi Blanc de prendre l'opposition et non de la céder.
La solution reposait donc bien sur l'opposition et non sur l'anti-opposition.
|
|
|
@Erony
J'attends la sortie de la dernière mouture de votre livre sur les finales pour me faire à ces concepts de finales qui sont encore pour moi un peu barbares.
Si on peut déjà le commander c'est qu'il va bien sortir un jour.
De plus il est donné.
|
|
|
Tant que je suis par là.
@Tantale concernant l’étude de Weenink 1924 (08/09/2012 - 08:08:02) :
l’étude repose sur l’opposition. Il est donc bien question de cases conjuguées “bien qu'il ne s'agisse que d'opposition”.
Cette “opposition” non justifiée entre Opposition et Cases conjuguées est également présente sur ta page web.
|
|
|
Ok je supprime la phrase "Here not corresponding squares but opposition"
|
|
|
@erony concernant la classification des différents cas de conjugaison (dans les Finales de Pions) (08/09/2012 - 12:20:01)
N’ayant malheureusement pas réussi à accéder aux vieux grimoires d’origine, je n’ai pu que déduire la classification d’Halberstadt en 8 cas [symétrie Diagonale ou Horizontale (en fait “Verticale” dans le texte consulté) + translation de 0 à 3 cases] à partir de ce que j’ai pu trouver dans ce numéro de British Endgame Study News.
Zinar ne classe pas les différents cas en fonctions de la disposition des zones de conjugaison l’une par rapport à l’autre, mais en fonction de leur structure géométrique.
Il distingue ainsi :
1) le système à 8 Cases, qui peut être considéré comme une extension du système Quadratique (voir dans ce fil Locock 1892; Bianchetti 1925)
2) le système Quadratique, ou Triangle-Carré car il peut être considéré comme une extension du système Triangulaire plus réduit (voir dans ce fil Lasker/Reichhelm 1901)
3) le système Quadratique avec cases de l’arrière ambiguës, qui peut-être considéré comme un système intermédiaire entre le système Quadratique et le système Triangulaire
4) le système Triangulaire, qui est le système le plus réduit parmi ces 4 systèmes apparentés
5) les combinaisons de Deux Systèmes dans différentes parties de l’échiquier (8-Cases + Quadratique, Quadratique + Quadratique, etc.)
6) le système Rectangulaire à 6 Cases, qui peut être considéré comme la superposition partielle de deux systèmes Quadratiques. Si les zones sont disposées de façon symétrique horizontalement ou verticalement, et sans décalage de colonne ou de rangée (Halberstadt aurait dit 0V ou 0H), ce système peut être résolu avec les Règles de l’Opposition (voir dans ce fil Bianchetti 1926).
7) le système “T” . Dans les systèmes précédents, les zones des deux camps étaient superposables. Ce n’est plus le cas avec le système T (nom donné par Bähr mais étude princeps due à Sacconi) où la zone a la forme d’un T dans un camp et d’un carré dans l’autre camp (avec une numérotation inversée par rapport au système Quadratique).
8) les systèmes “Multi-Cases” , qui peuvent être considérés comme des extensions ou des superpositions partielles de différents systèmes vus précédemment.
- Sont d’abord décrits des systèmes dans lesquels les zones des deux camps sont “superposables” : le système Rectangulaire à 8 Cases (système Rectangulaire à 6 Cases + système Quadratique), le système à 10 cases (système à 8 Cases + système Quadratique), le système à 13 Cases (système à 8 Cases + système à 8 Cases; voir dans ce fil Ebersz 1930)
- Sont ensuite décrits des systèmes dans lesquels un des camps disposent de cases supplémentaires (“excès de correspondance”) : système à 8 Cases + système Quadratique, système Rectangulaire à 6 Cases + système Quadratique. L’excès de correspondance autorise le plus souvent des erreurs qui sont ici rattrapables.
Les trois dernières catégories sont moins clairement définies.
("J'ai toujours un tiroir intitulé Choses inclassables ailleurs ... ce sont parmi les choses les plus intéressantes" B. Vian)
9) les systèmes Irreguliers, qui peuvent être considérés comme équivalents aux systèmes précédents mais ou au moins une des zones présente une ou plusieurs cases décalées (zone Rectangulaire à 6 Cases vs zone Rectangulaire à 6 Cases avec décalage; zone à 10 Cases vs zone à 10 Cases avec décalage).
10) les systèmes de Second Ordre, parfois très complexes car ils tiennent compte de temps de reserve dont dispose en général le camp le plus fort.
11) des exemples de cas compliqués, de part l’analyse de la position (possibilités de contre-attaque, etc.), mais dont les systèmes de conjugaison retombent dans les cas déjà répertoriés.
Au final, je serais tenté de préférer la classification de Zinar aussi bien sur le plan théorique qu’heuristique. Il me paraît en effet plus facile de dégager des règles et des modes opératoires adaptés, en se basant sur la structure des zones de conjugaison plutôt que sur leurs dispositions relatives. Ces derniers éléments purement descriptifs peuvent en revanche s’avérer d’une grande utilité pratique quand il s’agit de faciliter le repérage visuels entre cases conjuguées (même couleur ou couleurs opposées, décalages de colonnes ou de rangées).
|
|
|
@erony concernant la classification des différents cas de conjugaison (dans les Finales de Pions) (08/09/2012 - 12:20:01)
N’ayant malheureusement pas réussi à accéder aux vieux grimoires d’origine, je n’ai pu que déduire la classification d’Halberstadt en 8 cas [symétrie Diagonale ou Horizontale (en fait “Verticale” dans le texte consulté) + translation de 0 à 3 cases] à partir de ce que j’ai pu trouver dans ce numéro de British Endgame Study News.
Zinar ne classe pas les différents cas en fonctions de la disposition des zones de conjugaison l’une par rapport à l’autre, mais en fonction de leur structure géométrique.
Il distingue ainsi :
1) le système à 8 Cases, qui peut être considéré comme une extension du système Quadratique (voir dans ce fil Locock 1892; Bianchetti 1925)
2) le système Quadratique, ou Triangle-Carré car il peut être considéré comme une extension du système Triangulaire plus réduit (voir dans ce fil Lasker/Reichhelm 1901)
3) le système Quadratique avec cases de l’arrière ambiguës, qui peut-être considéré comme un système intermédiaire entre le système Quadratique et le système Triangulaire
4) le système Triangulaire, qui est le système le plus réduit parmi ces 4 systèmes apparentés
5) les combinaisons de Deux Systèmes dans différentes parties de l’échiquier (8-Cases + Quadratique, Quadratique + Quadratique, etc.)
6) le système Rectangulaire à 6 Cases, qui peut être considéré comme la superposition partielle de deux systèmes Quadratiques. Si les zones sont disposées de façon symétrique horizontalement ou verticalement, et sans décalage de colonne ou de rangée (Halberstadt aurait dit 0V ou 0H), ce système peut être résolu avec les Règles de l’Opposition (voir dans ce fil Bianchetti 1926).
7) le système “T” . Dans les systèmes précédents, les zones des deux camps étaient superposables. Ce n’est plus le cas avec le système T (nom donné par Bähr mais étude princeps due à Sacconi) où la zone a la forme d’un T dans un camp et d’un carré dans l’autre camp (avec une numérotation inversée par rapport au système Quadratique).
8) les systèmes “Multi-Cases” , qui peuvent être considérés comme des extensions ou des superpositions partielles de différents systèmes vus précédemment.
- Sont d’abord décrits des systèmes dans lesquels les zones des deux camps sont “superposables” : le système Rectangulaire à 8 Cases (système Rectangulaire à 6 Cases + système Quadratique), le système à 10 cases (système à 8 Cases + système Quadratique), le système à 13 Cases (système à 8 Cases + système à 8 Cases; voir dans ce fil Ebersz 1930)
- Sont ensuite décrits des systèmes dans lesquels un des camps disposent de cases supplémentaires (“excès de correspondance”) : système à 8 Cases + système Quadratique, système Rectangulaire à 6 Cases + système Quadratique. L’excès de correspondance autorise le plus souvent des erreurs qui sont ici rattrapables.
Les trois dernières catégories sont moins clairement définies.
("J'ai toujours un tiroir intitulé Choses inclassables ailleurs ... ce sont parmi les choses les plus intéressantes" B. Vian)
9) les systèmes Irreguliers, qui peuvent être considérés comme équivalents aux systèmes précédents mais ou au moins une des zones présente une ou plusieurs cases décalées (zone Rectangulaire à 6 Cases vs zone Rectangulaire à 6 Cases avec décalage; zone à 10 Cases vs zone à 10 Cases avec décalage).
10) les systèmes de Second Ordre, parfois très complexes car ils tiennent compte de temps de reserve dont dispose en général le camp le plus fort.
11) des exemples de cas compliqués, de part l’analyse de la position (possibilités de contre-attaque, etc.), mais dont les systèmes de conjugaison retombent dans les cas déjà répertoriés.
Au final, je serais tenté de préférer la classification de Zinar aussi bien sur le plan théorique qu’heuristique. Il me paraît en effet plus facile de dégager des règles et des modes opératoires adaptés, en se basant sur la structure des zones de conjugaison plutôt que sur leurs dispositions relatives. Ces derniers éléments purement descriptifs peuvent en revanche s’avérer d’une grande utilité pratique quand il s’agit de faciliter le repérage visuels entre cases conjuguées (même couleur ou couleurs opposées, décalages de colonnes ou de rangées).
|
|
|
Je remets la position de Grigoriev (1922)
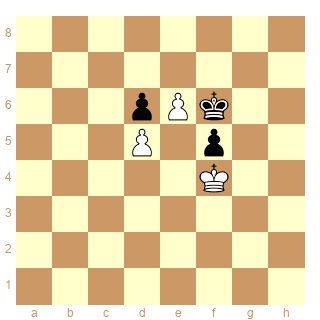
réponse au commentaire du 8 septembre à 21h44
Erony : Quelle est cette amélioration d'Halberstadt datant de 1936 ? C'est vrai, le Roi blanc peut aussi passer par e2 ; il s'agirait donc d'une bien mauvaise étude si c'en était une, mais ce n'est apparemment pas le cas :
- Elle n'a pas été présentée dans le texte original comme une étude et il est arrivé plus d'une fois à Grigoriev, dans ses investigations sur les finales, de proposer des positions sans unicité de solution.
- La phrase clé de la solution verbale de Grigoriev, après l'établissement des cases conjuguées, est "Le chemin le plus court vers la victoire pour les Blancs consiste à aller le plus vite possible en g2, sur quoi le Roi noir n'aura simplement pas de réponse." Après une telle explication, on peut même imaginer qu'il savait que le Roi blanc pouvait aller en e2 mais que son propos était simplement d'expliquer les cases conjuguées, thème de son article.
|
|
|
D'accord Kloch sur la préférence à une classification par structure. Resterait à illustrer chaque catégorie, en précisant les raisons de l'inclusion dans icelle, ce qui n'est pas de la tarte.
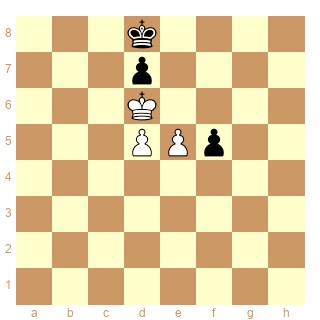
Je ne doute pas, Slucaino, que Grigoriev ait su où il allait avec cette "demi-étude". De même que Beasley, qui l'a pourtant incluse dans "Endgame magic". Le passage par g2 est en effet plus rapide, mais, sauf erreur, d'un temps seulement. Et l'on peut passer par h4 au lieu de h3. La version d'Halberstadt a aussi quelques défauts :
1.Rc5! Re7 2.Rd4 [2.Rc4] 2...d6 3.e6 Rf6 4.Re3 [4.Rd3] 4...Rg7 5.Rf2! [5.Rf4?! Rf6 redonne Grigo; 5.Rf3! Rg6 6.Rg2! Rf6 7.Rh3; 5.Re2! Rf6 6.Rf2! Rg6 7.Rf3] 5...Rf6 6.Rg2! Rg6 [6...Rg7 7.Rg3!] 7.Rf3 Rg7 8.Rg3! Rf6 [8...Rg6 9.Rh4! Rf6 10.Rh5] 9.Rf4! Rg6 10.e7! Rf7 11.Rxf5 Rxe7 12.Rg6 1–0
3k4/3p4/3K4/3PPp2/8/8/8/8
|
|
|
Mais il y a tellement d'études de Grigoriev qui n'ont aucun défaut ! Et nous avons tellement mieux pour "expliquer les cases conjuguées", par exemple la partie de Gulko ci-dessus qui, je le rappelle, transpose dans une étude de C. Costantini, 1979. Un cas de plus où la nature imite l'art !
|
|
|
Pour l'exercie de Frantisek Dedrle 1921 (merci Bibifoc),
Est-ce que mon diagramme est correct?
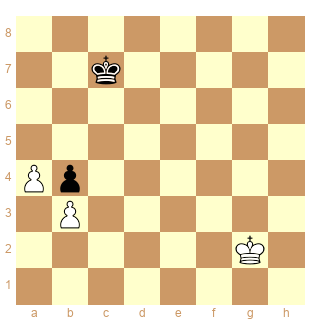
|
|
|
Non, vous devez supprimer le "1" sur c5 et surtout vider complètement les cases d4 et e4. L'accès de l'une de ces cases donne le gain aux Blancs, quel que soit le trait. Elles ne peuvent donc être "conjuguées" à qui que ce soit.
Et il faut ajouter des chiffres. Cases conjuguées : f3/d5, g3/e5, h3/d5, f4/d4, g4/e4, h4/d4, f5/d5, g5/e5, h5/d5, f6/d6, g6/e6, h6/d6, f7/d7, g7/e7, h7/d7. J'ai éliminé la 8e rangée : même s'il est vrai que f8 et d8 sont conjuguées, cela n'a pas beaucoup d'intérêt puisque l'opposition diagonale fonctionne, à Rf8 les Noirs peuvent répondre ...Rd6!.
Notez l'absence de g5/c5, g6/c6 et g7/c7 à cause... de l'interdiction de la case c4, qui casse aussi une partie de l'opposition rectangulaire ! Que l'on retrouve tout de même dans h3/d5 : souvenez-vous, un rectangle dont chaque côté fait un nombre impair de cases.
D'autre part, g2 et d6 ne sont pas conjuguées (pas plus que h2 et e6) même si parfois, à Rg2 il faut pouvoir répondre ...Rd6!!. En effet, trait aux Noirs, ...Rd6-e6! annule.
Je n'ai sans doute pas terminé, mais vous avez du grain à moudre.
|
|
|
J'avais oublié les plus évidentes : d3/d5, e3/e5. Aucune case de la 2e rangée car les Noirs font barrage par ...Rd4-e4 dans tous les cas. Ou, comme déjà dit, restent en observation par ...Rd6-e6.
Une allusion à cette étude est ici le 16/01/2008 à 20:50. Un autre lien fait aussi honneur à Dedrle : il améliore l'étude de Weenink deux ans plus tard. On y trouve aussi celle de Neustadtl, dont je parlais, quoique attribuée à Capa (on ne prête qu'aux riches).
Ne me remerciez pas, ou alors, soyez le grateful dedrle (dédié à PE).
|
|
|
Le graphique précédent était complètement faux (j'avais raisonné trait aux blancs)
celui-ci établi en suivant vos indications devrait être correct.
|
|
|
Merci Erony pour avoir détaillé l'étude d'Halberstadt qui présente sous un autre angle la position de Grigoriev.
C'est vrai qu'il existe bien des études, et même des parties, plus fines et jolies que l'exemple de Grigoriev pour illustrer en détail les cases conjuguées.
Pourtant, cette position possède à mes yeux des qualités graphiques importantes pour présenter les cases conjuguées à ceux qui ne les connaissent pas :
- la totalité de l'espace de manoeuvre du Roi noir (f6, g6 et g7) se trouve reflétée dans le camp blanc et à portée du Roi s'il se trouve en g2 (f3, g3 et h3).
- La case g2 est éloignée de l'action.
Je connais aussi par expérience personnelle l'intérêt pédagogique de cette position, car elle m'a tout simplement émerveillé il y a bien longtemps, et cela m'a donné un accès plus facile au monde des cases conjuguées qui m'apparaissait alors comme un peu rébarbatif.
Ainsi, cette position de Grigoriev n'est pas le meilleur choix pour étudier les cases conjuguées en détail mais paraît excellente pour une introduction. C'est en tous cas de cette façon que Grigoriev lui-même s'en est servi.
En toute subjectivité, bien sûr.
|
|
|
Cette étude de Vitaly Halberstadt - 1930 - Les Blancs jouent et gagnent accompagné du croquis d'Halberstadt ne serait-elle pas démolie (elle ne l'est pas dans HHDB)
[Event "Ceskoslovensky Sach#328"]
[Site "?"]
[Date "1930.??.??"]
[Round "?"]
[White "Halberstadt=V"]
[Black "(+0000.77b2c8)"]
[Result "1-0"]
[Annotator ",JMRW"]
[SetUp "1"]
[FEN "2k5/2p2p2/2p1p3/2P1PpP1/1p1P1p2/1P3P2/1K3P2/8 w - - 0 1"]
[PlyCount "35"]
[EventDate "1930.??.??"]
{Ceskoslovensky Sach/11} 1. Kb1 $144 $1 (1. Kc2 $144 $1 Kb7 2. Kd3 Ka6 3. Ke2
Kb7 4. Kf1 Kc8 5. Kg2 Kd8 6. Kh3 Ke8 7. Kh4 Kf8 8. Kh5 Kg7 9. g6 fxg6+ 10. Kg5
Kh7 11. Kf6 g5 12. Kxe6 g4 13. Kf7 g3 14. e6 gxf2 15. e7 f1=Q 16. e8=Q Qg1 17.
Qxc6 Qg8+ 18. Ke7 Qg7+ 19. Ke6 Qg8+ 20. Ke5 Qd8 21. Qf6 Qe8+ 22. Kxf4 Kg8 23.
Kxf5 $18) (1. Kc1 $144 $1 Kb7 2. Kc2 Ka7 3. Kd1 Kb8 4. Ke2 Kb7 $18) 1... Kb8 2.
Kc1 Ka8 3. Kd1 Kb8 4. Ke1 Kc8 (4... Kb7 $144 5. Ke2 $1 $18) (4... Ka8 $144 5.
Kf1 $1 Kb8 6. Kg2 Kc8 7. Kh3 Kd8 8. Kh4 Ke8 9. Kh5 Kf8 10. g6 Kg7 11. gxf7 Kxf7
12. Kh6 Kf8 13. Kg6 Ke7 14. Kg7 Ke8 15. Kf6 Kd7 16. Kf7 $18) 5. Kd2 (5. Kf1
$144 Kb7 6. Kg2 Kc8 7. Kh3 Kd8 8. Kh4 Ke8 9. Kh5 Kf8 10. Kh6 Kg8 11. g6 Kf8 12.
Kh7 fxg6 13. Kxg6 Ke7 14. Kg7 Ke8 15. Kf6 Kd7 16. Kf7 $18) 5... Kb7 6. Ke2 Kc8
7. Kd3 Kb7 8. Kc4 Ka6 9. Kxb4 Ka7 10. Ka5 Kb7 11. b4 Ka7 12. b5 cxb5 13. Kxb5
Kb7 14. c6+ Kc8 15. Ka6 Kb8 16. d5 exd5 17. g6 fxg6 18. e6 $18 1-0

|
|
|
@erony (09/09/2012 - 09:19:56) concernant la classification de Zinar
Le défi lancé par erony laisse en effet entrevoir peu de tarte mais beaucoup de pain sur la planche, même en se contentant de reprendre les explications et les exemples de Zinar.
L'impossibilité d'inclure plus d'un diagramme, ainsi que des diagrammes annotés (ou des images) rend ladite planche un peu plus savonneuse.
Je verrai ce que je peux faire. Avec le temps.
Pour les plus impatients je peux discrètement adresser une version pdf détaillée de l'article de Zinar (en anglais) que le copyright m'interdit sans doute de diffuser publiquement en intégralité.
Une adresse figure dans mon profil.
|
|
|
A l'aide !
Pour cette étude de Walter Bähr:
[Event "Mainfränkische Zeitung"]
[Site "?"]
[Date "1934.12.21"]
[Round "?"]
[White "Bahr=W"]
[Black "(+0000.54f1f7)"]
[Result "1-0"]
[SetUp "1"]
[FEN "8/5k2/2p1p3/2P1Pp1p/7P/6P1/6P1/5K2 w - - 0 1"]
[PlyCount "12"]
[EventDate "1934.??.??"]
1. Ke1 Ke7 2. Kf2 Kf8 3. Ke2 Ke7 4. Kf3 Kf7 5. Ke3 Kg6 6. Kf4 Kh6 1-0
Trait aux noirs voici les cases correspondantes
Mais comment les établit-on trait aux blancs?

|
|
|
Est-ce que quelqu'un a une opinion sur
- "The Final Countdown" de Herman Claudius Van Riemsdijk et Willem Diederik Hajenius
- "The Tactics of End-Games" de Ban, Jeno; Broché?
|
|
|
Pour cette étude de Thomas Dawson - 1921 - Les Blancs jouent et gagnent,
Quelles sont les cases correspondantes?
[Event "2.p The Chess Amateur#0811"]
[Site "?"]
[Date "1921.??.??"]
[Round "?"]
[White "Dawson=T"]
[Black "(+0000.66e1b6)"]
[Result "1-0"]
[Annotator ",JMRW"]
[SetUp "1"]
[FEN "8/4p1p1/1k2p1p1/p3P1P1/P1p2P2/2P5/5P2/4K3 w - - 0 1"]
[PlyCount "25"]
[EventDate "1921.??.??"]
{The Chess Amateur/7 1922} 1. Kd1 $1 (1. Ke2 $143 Kc5 2. Ke3 Kd5 3. f3 Kc5 4.
Ke4 Kc6 5. Kd4 Kb6 6. Kxc4 Kc6 7. Kd4 Kb6 8. c4 Kc6 9. c5 Kc7 10. Kc4 Kc6 11.
f5 gxf5 12. g6 (12. f4 $144 g6 $11) 12... f4 $1 13. Kd4 Kc7 14. Ke4 Kc6 15. Kd4
(15. Kxf4 $143 Kxc5 16. Kg5 Kb4 17. f4 Kxa4 18. f5 exf5 19. Kxf5 Kb3 20. Ke6 a4
21. Kxe7 a3 22. Kf7 a2 23. e6 a1=Q $19) 15... Kc7 $11) 1... Kc6 2. Kd2 Kc5 3.
Ke2 Kc6 4. Kf3 Kb6 5. Ke3 Kc5 6. Ke4 Kc6 7. Kd4 Kb6 8. Kxc4 Kc6 9. Kd4 (9. Kd3
$144 Kd5 10. c4+ Kc5 11. Kc3 Kb6 12. Kd4 Kc6 $18 {loss of time}) 9... Kb6 10.
c4 (10. Kd3 $144 Kc5 11. c4 Kb6 12. Kd4 Kc6 $18 {loss of time}) 10... Kc6 {Win}
11. c5 (11. f5 $144 exf5 12. c5 Kc7 13. Kd5 Kb7 14. Ke6 Kc6 15. Kxe7 $18) 11...
Kc7 12. Kc4 (12. Kd3 $144 Kb7 13. Kc4 Kc6 14. f3 $18 {loss of time}) (12. f5
$144 gxf5 13. Kc4 Kc6 14. g6 f4 15. f3 Kb7 16. Kb5 $18) 12... Kc6 13. f3 $18 (
13. f5 $144 exf5 14. Kd4 e6 15. Kc4 f4 16. f3 Kc7 17. Kb5 $18) 1-0

|
|
|
Pour cette étude de Vitaly Chupin 1982 - Les blancs jouent et font nulle, voici les cases conjuguées
Il n'y a que les deux Rois mobiles et c'est déjà un casse-tête!

|
|
|
Il serait intéressant aussi de trouver les cases correspondantes pour cette étude de Mikhail Zinar - Les Blancs jouent et gagnent - 1975

|
|
|
@Tantale (11/09/2012 - 10:51:48)
Comme je l'avais signalé le 02/09/2012 (15:15:58), cette étude de Chupin n'est pas originale du point de vue de sa résolution puisqu'elle utilise, aux symétries près, exactement le même réseau de cases conjuguées que Bianchetti dans l'étude de 1925 présentée plus haut.
Elle a en revanche le mérite d'illustrer le fait que la connaissance des règles de conjugaison ne permet pas seulement au camp en supériorité de gagner, elle permet aussi parfois au camp en infériorité de se défendre.
Incidemment, elle permet aussi de souligner que le réseau de cases conjuguées, qui découle de positions de zugzwang réciproque, dépend directement de la structure de Pions et est indépendant du trait dans la mesure où le trait n'affecte pas cette structure.
Du coup je me demande, Tantale, si tu as trouvé la réponse à ta question du 10/09/2012 - 16:49:19.
|
|
|
@Kloch
Pour l'étude de Walter Bähr (10/09/2012 - 16:49:19)
oui j'ai compris mais je trouve qu'il est plus facile d'établir les cases conjuguées trait aux noirs (ce sont bien sur les mêmes trait aux noirs ou trait aux blancs).
Le jeu complet des cases conjuguées devrait être celui-là
Trait aux blancs: il faut aller sur un numéro que les noirs ne peuvent pas atteindre.
Trait aux noirs: il faut aller sur le même numéro que celui où est le Roi blanc.
Pour l'étude de Vitaly Chupin je suis d'accord aussi mais pourquoi écrivent-ils dans EG80 à propos de cette étude 5569 « An extension in depth and breadth of Bianchetti's study of 1925 »?
|
|
|
@Kloch ton email ne semble pas valide.
|
|
|
Chupin vs Bianchetti.
La piste de danse est la même, la musique est la même, seul le Roi qui conduit a changé.
Même si la création n'est pas totalement originale, l'impression esthétique peut tout à fait être différente. Affaire de goût.
Pour mon e-mail, je pense avoir rectifié mon erreur hier soir (.com au lieu de .fr)
|
|
|
@Reyes
Je ne comprends pas pourquoi mes posts disparaissent
J'ai posté ceci qui a été effacé:
-----------
Pour cette étude de Zinar 1975 - les Blancs jouent et gagnent, j'ai dressé le croquis des cases correspondantesw.
Est-ce juste?
Est-ce complet?
[Event "Krimskaja Pravda"]
[Site "?"]
[Date "1975.??.??"]
[Round "?"]
[White "Zinar"]
[Black "(+0000.36g8a8)"]
[Result "1-0"]
[Annotator ",JMRW"]
[SetUp "1"]
[FEN "k5K1/8/8/4p1p1/1p2p1p1/1p2P1P1/1P6/8 w - - 0 1"]
[PlyCount "15"]
[EventDate "2012.??.??"]
1. Kg7 (1. Kf7 $143 Kb7 $1 2. Kf6 Kb6 $1 3. Ke6 Kc6 $1 4. Kxe5 Kc5 $1 5. Kxe4
Kc4 $1 6. Kf5 Kd3 $1 7. e4 Kc2 $1 8. e5 Kxb2 $1 9. e6 Kc3 10. e7 b2 $1 11. e8=Q
b1=Q+ $1 $11) (1. Kf8 $143 Kb8 $1 2. Ke8 Kc8 $1 3. Ke7 Kc7 $1 4. Ke6 Kc6 $1 $11
) 1... Ka7 (1... Kb7 $144 2. Kf7 $18) 2. Kg6 Kb6 3. Kf6 (3. Kxg5 $143 Kc5 4.
Kf5 Kd5 $17) 3... Kb5 4. Kf5 (4. Kxe5 $143 Kc5 $1 5. Kxe4 Kc4 $1 6. Kf5 Kd3 $1
7. e4 Kc2 $1 8. e5 Kxb2 9. e6 Kc3 10. e7 b2 $1 11. e8=Q b1=Q+ $1 $11) 4... Kc6
(4... Kc5 $144 5. Kxe5 $18) 5. Ke6 (5. Kxg4 $143 Kd5 6. Kf5 g4 $17) (5. Kxe4
$143 Kd6 6. Kd3 Kd5 $17) 5... Kb6 6. Kd6 Kb5 7. Kd5 {win} Kb6 8. Kxe4 $18 (8.
Kc4 $144 Kc6 9. Kxb4 $1 $18) 1-0
-----------
Y a-t-il quelque chose qui enfreint la charte?

|
|
|
Voilà que le lien vers le croquis a été détruit.
|
|
|
Puisque j' n'ai pas de réponse je remets le croquis des cases correspondantesafin que le post précédent soir compréhensible.
|
|
|
Je ne regretterais pas les quelques heures passées à lire et analyser la méthode présentée par Kloch.
Toute la difficulté étant maintenant de réaliser ces analyses de tête :)
|
|
|
Ce qui m'a surpris c'est l'absence de pertinence de tous les modules d'analyse.
Comme il y a peu de coups légaux avec les pions bloqués je m'attendais à ce que l'arbre d'analyse n'explose pas et que la réponse des modules soit quasi-immédiate.
Hors souvent les modules ne trouvent pas ou donnent même des résultats erronés.
|
|
|
merci Ofkrad ... ^^
|
|
|
Après s’être consacré à la création et à la peinture qui l’ont rendu célèbre, Marcel Duchamp est devenu un joueur d’échecs à part entière, d’un excellent niveau, dont la carrière est , elle, paradoxalement plutôt inconnue du grand public.
En effet, vers 1918 au fait de sa gloire, il se retire du monde de l’art et se passionne intensément pour le " noble jeu ".
Il participe même au tournage du film avant-gardiste Entr'acte de René Clair. Dans la première scène du film, il joue aux échecs avec Picabia sur le toit du théâtre des Champs-Elysées.
Parmi une multitude de prestations échiquéennes, ce personnage exceptionnel a participé entre 1923 et 1935, à plus de trente compétitions officielles , tant nationales qu’internationales, dont cinq championnats de France , quatre olympiades et neuf tournois internationaux. Egalement chroniqueur d’échecs au journal parisien Ce soir et nommé maître de la Fédération Française d’Echecs, Marcel Duchamp a co-signé en 1932 un ouvrage théorique remarquable en trois langues : l’opposition et les cases conjuguées sont réconciliés. Un livre, depuis longtemps introuvable que seuls quelques rares collectionneurs possèdent. .
Tous les joueurs d’échecs sont des artistes
Tel était l’avis de Marcel Duchamp qui l’expliquait ainsi : " Dans les échecs, la beauté n’est pas une expérience visuelle, comme en peinture. C’est une beauté plus proche de celle qu’offre la poésie " .
Marcel Duchamp a poussé très loin la recherche d’une convergence entre les échecs et l’art au point de mettre en concurrence ces deux pratiques, faisant d’une part de sa vie de joueur son œuvre et pensant d’autre part les échecs comme un éventuel horizon de l’art.
À lire aussi
Le rapprochement entre art et échecs ménage quelques surprises. Si, tels des joueurs connus comme Le Lionnais ou Aaron Nimzowitch, on peut adopter une approche esthétique sur les échecs, le style de jeu de Marcel Duchamp, contrairement à ce qu’on pourrait attendre, n’avait rien d’extravagant. Plutôt conformiste, Marcel Duchamp était loin d’être aux échecs ce qu’il était pour l’art. La place que Duchamp voulait réserver aux échecs dans l’art résidait dans une projection de l’esthétique au niveau cérébral : la beauté serait " entièrement dans la matière grise ".
Beauté non visuelle, non sensible, elle serait en fait déclenchée par un mouvement cérébral dont le ressort reposerait sur la signification des déplacements et des rapports dynamiques des pièces les unes par rapport aux autres.
Avec Marcel Duchamp, un pouvoir d’évocation est attribué aux échecs en complément d’une option esthétique inédite.
Né le 8 juillet 1887, mort le 2 octobre 1968, Marcel Duchamp est resté un artiste atypique jusqu’au bout puisqu’il avait demandé à être enterré à Rouen sous cette épitaphe : " d’ailleurs, c’est toujours les autres qui meurent "
[Texte de Frederic Chomier]
Voici une video dans laquelle on voit Marcel Duchamp
|
|
|
Vlastimil Fiala "The chess biograpy of Marcel Duchamp" Volume one : 1887-1925, Volume two : 1926-1930
|
|
|
J'ai exploité le document de Zinar concernant les cases conjuguées dont parle Kloch.
Ce document est d'une grande valeur même s'il comporte quelques erreurs. J'ai donc sauté quelques études incorrectes.
Voici le résultat
|
|
|
Dans ce fil (Cases conjuguees par DrZen le 04 juillet 2006) J'ai trouvé cette étude de Jan Folty 1931 - les blancs jouent et gagnent - pour laquelle petieglise avait brillamment trouvé les cases conjuguées en moins de cinq minutes.
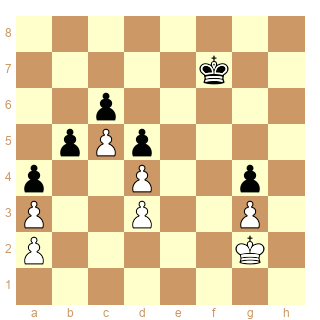
|
|
|
Incroyable, j'y suis arrivé...
Tout comme la résolution de la position de la partie Neustadt-Porges (1901). trait au blancs.

|
|
|
@Flytox: la solution de la partie de Neustadt-Porges (1901) trait au blancs ne me semble pas passer par les cases conjuguées (?)
|
|
|
@Tantale,
si je ne m'abuse, il y a bien 3 positions de zugzwang réciproque autour de la case d4 :
- Re3/Rd5 (la position actuelle)
- Re4/Rc5
- Rf3/Rc6
Dans la position actuelle (trait aux Blanc) les Noirs ont la conjugaison et si les Pions étaient bloqués (par ex PB en h4 au lieu de h2), ils tiendraient la nulle car je ne vois pas de manœuvre possible pour les Blancs vers l'arrière du Triangle.
Le second écueil pour les Blancs, c'est que même si le Roi parvient en d4, il y a encore une défense pour les Noirs par Rb5.
Mais les Blancs ont 2 temps de réserve (h2-h3 et h3-h4) : le premier leur sert à parvenir en d4 (après avoir optimisé la position du Roi Blanc (il faut choisir la position de zugzwang la plus favorable : Re4/Rc5) et le second à gagner le Pion c4.
Bien sûr il faut vérifier les variantes où ce sont les Noirs qui avancent leur pion h et calculer si le Roi Blanc a le temps d'aller le prendre et de percer à l'aile-Roi avant la contre-attaque du Roi Noir sur les Pions de l'aile-Dame.
|
|
|
Ceci dit, si mon analyse précédente est juste, la solution semble assez linéaire et c'est vrai qu'avec un peu de calcul on peut se passer des cases conjuguées pour trouver la suite gagnante (le choix n'est pas énorme).
Elles ont tout de même à mon avis le mérite d'offrir une approche rationnelle et d'expliquer pourquoi les Blancs sont gagnants.
|
|
|
@Kloch
Il semble que Re5/Rd5 (la position actuelle) par exemple, les Blancs gagnent quelque soit le trait.
Ce ne serait donc pas des cases de zugzwang réciproque.
|
|
|
@Kloch
J'ai demandé à Sergiy Didukh si le texte de Zinar était sous copyright (il connait Zinar).
Il m'a répondu qu'il était sur que non.
Je vais donc les prochains jours rajouter ses explications sur comment trouver les cases correspondantes.
|
|
|
Ce n'est pas parce que les Blancs gagnent quel que soit le trait qu'il n'est pas question de cases conjuguées et donc de cases de zugzwang réciproque (puisque c'est bien la définition la plus simple qu'on en donne en général, ... avant de développer ... surtout moi).
D'ailleurs on peut tout aussi bien imaginer des positions de nulle quel que soit le trait avec pourtant des cases conjuguées.
Avoir la conjugaison ne garantit pas le gain (ou la nulle), et de manière générale ne signifie pas que l'issue de la partie sera différente selon le trait; c'est une façon de parvenir à un objectif précis qui est en général d'atteindre une ou certaines cases clés.
Si tu considères un cas élémentaire de conjugaison où le camp en supériorité l'emporte par une manœuvre de triangulation (de mémoire je crois qu'on donne la position Fahrni-Alapin comme exemple bateau), tu constateras que les Blancs l'emportent quel que soit le trait, mais que dans un cas ils ont besoin de perdre 1 temps pour y parvenir (la fameuse manœuvre de triangulation à l'arrière sur des cases qui n'ont pas d'équivalent dans le camp des Noirs, c-à-d dont les cases conjuguées de façon non ambiguë n'existent pas).
Pourquoi les Blancs doivent-ils perdre un temps ? Justement parce qu'ils ont besoin de rendre le trait pour gagner la conjugaison.
Idem dans le cas présent, la première perte de temps dont a besoin le Roi Blanc est fournie par un mouvement de Pion et non de Roi, mais l'idée est la même. Tout ceci pour permettre au Roi Blanc de gagner la conjugaison sur les cases de ZZ réciproque que j'ai données, et d'atteindre ainsi d4 qui était son premier objectif.
|
|
|
Pourquoi ne serait-il pas protégé ?
En tout cas le support (livre, CD) est commercialisé et les auteurs sont en vie.
|
|
|
Voici l'email de Didukh, compatriote de Zinar et un de ses amis :
"Hi,
I'm sure the text is not copyrighted. Nothing to worry about.
Keep on doing nice work!
Best wishes,
Sergiy"
|
|
|
Ce serait avec grand plaisir si Sergiy pouvait transmettre mes remerciements à M. Zinar pour son travail exceptionnel (et unique à ma connaissance).
Ce n'est pas ironique du tout.
Se doute-t-il de l'intérêt qu'il suscite encore ? (je ne veux pas dire en nombre comme sur facebook, je veux parler d'intensité ou de profondeur de l'intérêt)
|
|
|
Voici l'email de Sergiy: myseds@i.ua
|
|
|
Justement Kloch, pour les cas tels que "Fahrni-Alapin" et Neustadtl-Porges, je proposais (ci-dessus le 08/09/2012 à 18h01) pour éviter cette confusion, le terme de cases semi-conjuguées (en attendant mieux), réservant celui de conjuguées aux cas où le trait donne, aux deux camps, le pire résultat.
Flytox : vous avez trouvé Foltys et Neustadtl, bravo ! Car le 9e coup du premier ne saute pas aux yeux, et la variante principale du second fait tout de même 27 coups, si je ne me trompe !
|
|
|
Étude de Botvinnik 1939 - Les Blancs jouent et gagnent.
Quelles sont les cases conjuguées?

|
|
|
Pour moi les cases conjuguées pour la position ci-dessus sont:
- b7/f5 b7/f7
- b6/f6
- c6/e6
- c7/e7 c7/e5
Est-ce juste?
|
|
|
Grigoriev le fameux compositeur était aussi un grand joueur témoin cette partie Grigoriev - Alekhine 1915
|
|
|
Before his departure from Russia in 1921, Alekhine played a match with Grigoriev of 7 games resulting in 2 wins and 5 draws in favour of Alekhine. Analyzing the match, Levenfish said: "In some of the games only exceptional ingenuity saved Alekhine from destruction."
|
|
|
Dans cette étude de Franz Sackmann - 1912 - Les Blancs jouent et gagnent,
Quelles sont les cases conjuguées?

|
|
|
Ref Botvinnik 1939 (le 14/09/2012 - 22:22:10)
Pour moi les cases critiques du Pion d5 (= cases dont l’occupation par le Roi Blanc garantit le gain du Pion quel que soit le trait) sont e5-f5-g5 latéralement et d6-d7 vers l'arrière.
Ces cases critiques peuvent donc être considérées comme des cases clés pour le Roi Blanc si son objectif est de gagner le Pion d5.
En l’occurrence, le Roi Blanc peut donc effectivement gagner ce Pion d5 directement puisqu’il occupe déjà la case g5.
Par exemple 1.Rf5 Rc7 2.Re5 Rc6 3.Re6 et le Pion tombe.
Sauf qu’après la prise du Pion d5, les cases clés du Pion Blanc passé d4 (= cases dont l’occupation par le Roi Blanc garantit la promotion du Pion quel que soit le trait) sont c6-d6-e6.
[Les cases clés des Pions Passés en fonction de leur position sont décrites dans la plupart des manuels de finales (ou ici); mieux vaut les connaître, après avoir éventuellement vérifié par soi-même leur bien fondé, histoire d’en avoir le cœur net et d’éviter de croire qu’il s’agit d’une vérité révélée ou qu’il y a de la magie là-dessous.]
Les cases clés étant ici 3 cases voisines alignées, la lutte pour leur occupation s’inscrit dans un système de conjugaison rectangulaire qui obéit aux règles de l’Opposition.
De ce fait, si après la prise du Pion d5, le Roi Noir se place en d7 (par exemple 3...Rc7! 4.Rxd5 Rd7!), il obtient la conjugaison et le Roi Blanc ne pourra pas conduire son Pion à la promotion.
[Bien sûr 3…Rd7? de suite ne va pas car après 4.Rxd5 c’est le Roi Blanc qui aurait l’opposition et pourrait conduire son Pion d à la promotion]
La position serait donc nulle sans les Pions sur la colonne a.
Mais dans le cas présent, le Roi Blanc peut tout de même encore aller prendre les Pions a5 et a6 en sacrifiant le Pion d. On note néanmoins que le Pion a6 interdit la case b5 au Roi Blanc. Pour progresser, les Blancs doivent donc avancer leur Pion d : 5.Rc5 Rc7! 6.d5 Rd7 7.Rb6.
Mais j’ai alors l’impression que le Roi Blanc n’aura pas le temps d’occuper ensuite une des cases clés du Pion passé a4 (c-à-d b7-b8) : 7…Rd6 8.Rxa5 Rxd5 9.Rxa6 Rc6 nulle
Je crois en revanche que cette ligne serait gagnante pour les Blancs :
- si on retirait le Pion a6 : 5.Rc5 Rc7 6.Rb5 Rd6 7.Rxa5 Rd5 9.Rb6 Rxd4 10.a5 +-
- si on décalait tout d’une colonne vers la droite car après 1.Rg5 Rd7 2.Rf5 Rd6 3.Rf6 Rd7 4.Rxe5 Re7 5.Rd5 Rd7 6.e5 Re7 7.Rc6 Re6 8.Rxb5 Rxe5 9.Rxb6 Rd6 le Roi Blanc occupe une des cases clés du Pion passé b4 qui sont a6-b6-c6.
Les Blancs ont-ils mieux en s’en prenant d’abord aux Pions Noirs a6 et a5 au lieu de d5 ?
On peut assez facilement se rendre compte que c’est le cas, car si le Roi Blanc parvient à prendre les Pions a6 puis a5, il pourra ensuite facilement gagner le Pion d5 avec une position gagnante (qui est en fait au moins aussi avantageuse que la suite mentionnée plus haut après la prise Rxd5 à partir de la position initiale sans le Pion a6).
Il reste maintenant à voir comment procéder pour attaquer les Pions a6-a5, tout en vérifiant les éventuelles possibilités de contre-attaque du Roi Noir sur le Pion d4.
Recherchons tout d’abord les cases critiques.
Il me semble que toutes les cases du carré c6-c8-a8-a6 peuvent être considérées comme des cases critiques pour les Pions a6-a5 (en tout cas une fois une de ces cases occupée par le Roi Blanc, je ne vois pas d’où le Roi Noir pourrait défendre ses Pions).
La ligne frontière par rapport au Roi Blanc qui devra arriver par l’aile-Roi est représentée par les cases c6-c7-c8.
Il s’agit à nouveau de 3 cases voisines alignées, dont la lutte pour l’occupation s’inscrit dans un système de conjugaison rectangulaire qui obéit aux règles de l’Opposition.
En d’autres termes, sur chacune des 6ème, 7ème et 8ème rangées, les cases en opposition horizontale directe ou distante sont conjuguées (c-à-d les cases de même couleur sur chacune de ces 3 rangées, parmi lesquelles figurent bien les couples b7/f7, b6/f6, c6/e6 et c7/e7 données par Tantale, mais il y en a d’autres).
[Pour définir la limite réelle de la zone de conjugaison, il faut probablement vérifier certains cas extrêmes comme Rh6/Rf6 où le Roi Noir doit avoir des possibilités de contre-attaque]
Si on ne prend en compte comme unique objectif des Blancs que le gain des Pions a6-a5, le Roi Noir parvient encore à défendre la position puisqu’il lui suffit de rester sur la 7ème rangée et de prendre l’opposition sur la 6ème rangée dès que le Roi Blanc y pénètre.
La 6ème rangée est donc minée pour les deux Rois, ce qui avantage la défense.
Mais il ne faut pas perdre de vue un autre objectif important des Blancs qui est le gain du Pion d5 assorti du gain de la conjugaison autour des cases clés du Pion passé d4 (cases c6-d6-e6). C’est-à-dire le gain de l’opposition verticale directe (Rd5/Rd7).
Comme le Roi Noir doit rester en défense sur la 7ème rangée et que la 6ème rangée est minée, l’opposition diagonale directe (Re5/Rc7 signalée par Tantale, ou Rf5/Rd7) et l’opposition virtuelle(?) ou potentielle(?) (les deux Rois occupent le coin d’un rectangle dont les côtés comportent un nombre impair de cases = dont les coins sont des cases de même couleur) opèrent dans le cas présent.
Cela signifie que les cases g5 et c7 sont conjuguées, ainsi que les cases f5 et b7.
Cette dernière donnée devrait fournir la clé de l’étude : 1.Rf5!
Sans donner toutes les variantes, on peut indiquer les scénario suivants :
- si le Roi Noir reste sur la 7ème rangée (1…Rc7), le Roi Blanc prend le Pion d5 en gagnant l‘opposition verticale permettant de s’emparer ensuite des cases clés de son Pion passé d4 (2.Re5 Rd7 3.Rxd5 et le Pion d4 va a Dame)
- si le Roi Noir passe sur la 6ème rangée, le Roi Blanc s’empare de l’opposition horizontale et son objectif principal sera alors le gain des Pions a6-a5. Ceci peut intervenir au 1er coup (1…Rc6 2.Re6! ou 1…Rb6!? 2.Rf6!) ou plus tard (1…Rc7 2.Re5 Rc6 3.Re6)
Pour progresser dans ce dernier système d’opposition horizontale sur 3 rangées, il faut repérer la traverse principale qui est la 7ème rangée (ligne médiane du système) autour de laquelle le Roi Blanc doit contourner le Roi Noir.
Le Roi Blanc devra donc conserver la conjugaison (opposition horizontale) jusque sur la 7ème rangée et contourner ensuite le Roi Noir sur la traverse externe.
Par exemple :
1.Rf5! Rc7 2.Re5 Rc6 3.Re6 Rc7 4.Re7 (opposition sur la 7ème rangée)
et 4…Rc8 5.Rd6 (contournement) 5…Rd8 6.Rc6 Rc8 7.Rb6 Rb8 8.Rxa6 +-
ou 4…Rc6 5.Rd8 (contournement) 5…Rd6 6.Rc8 Rc6 7.Rb8 Rb6 8.Ra8 +- car le Pion a6 interdit l’accès au Roi Noir
|
|
|
Tiens, une étude de Moravec (1955) qui utilise le même décor que celle de Botvinnik 1939.

Cette étude enrichit la précédente par un préliminaire qui souligne une particularité de la position à laquelle il est fait allusion dans le tout dernier commentaire de mon post précédent.
A première vue je dirais que cela peut aussi mettre sur la piste de la solution de l’étude de Sackmann 1912.
|
|
|
Une autre de Maizelis,I (1956).
Gain
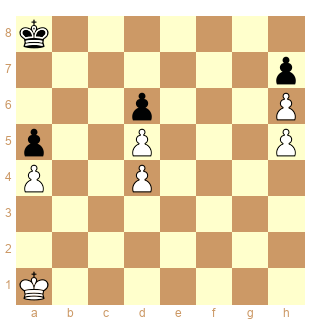
|
|
|
A Reyes
Encore un post que j'ai envoyé ce matin a été effacé ainsi que le fil de discussion (196 posts) qui l'hébergeait.
Quand on fait une recherche on obtient "cet article n'est plus disponible".
pourquoi?
|
|
|
Reyes exerce un petit pouvoir france-échiquéen! Ca lui fait du bien!
|
|
|
Tantale a raison, je vire tous les articles qui remontent à Mathusalem, que Tantale remontent juste pour placer un lien vers son site. A noter cependant que si Tantale connait parfaitement l'email de France-Echecs quand il se plante de rubrique ou pour réouvrir un article fermé aux commentaires, là, étrangement, il préfère poster sa réclamation dans l'article.
A part ça Salvador a tort, je ne viens plus que très rarement sur le forum et ce n'est certainement pas pour exercer un "pouvoir" quelconque, mais uniquement pour répondre aux demandes de quelques membres qui se fatiguent de voir la première page du forum à la gloire du site de Tantale.
|
|
|
@Reyes
- En l’occurrence le lien posté ce matin pointait vers une vidéo présentant 500 tableaux sur Youtube.
Certes elle est de moi mais le lien pointait sur youtube et non sur mon site.
- J'avais effectivement placé ce tableau sur Napoléon et Madame de Rémusat dans un fil datant de quelques années car j'y avais trouvé la partie qu'ils avaient disputée Y a-t-il un mal à cela? Quelle importance que ce fil soit récent ou ancien? Qu'elle importance que ce tableau provienne de mon site ou d'ailleurs?
- J'ai aussi posté voici trois semaines un fil de discussion sur "Les échecs et les mathématiques" qui n'a jamais été validé. Pourquoi?
- Auparavant le fil contenant le post qui ne plaisait pas était simplement clos. Maintenant ce fil disparaît entièrement (sur une recherche on obtient "ce sujet n'est plus accessible"). On brule pour une humeur la bibliothèque.
- De nombreux fils de discussion plus ou moins récents sont clos (avant toute intervention de ma part) ce qui empêche de placer son post à l'endroit où il a sa place.
- Mon email est dans mon profil. Je n'ai jamais été prévenu d'un acte de censure par cette voie.
Je me borne à constater qu'un article que j'ai écrit disparaît (en général dans les heures qui suivent).
On aurait par exemple pu m'écrire que le sujet sur les échecs et les mathématiques ne serait pas validé et m'en expliquer la raison.
- Reyes vous avez écrit sur ce forum à Chouia: "Ce que tu écris ne m'intéresse pas" et vous l'avez virée. Peut-être que d'autres gens étaient intéressés par ses articles qui du reste n'enfreignaient pas la charte.
Je sens que mon espérance de vie est limitée sur ce forum. Peut-être même celle de ce post.
|
|
|
J'adore la dernière phrase... Il ne manque qu'une petite larme...
|
|
|
@Kloch
Encore un travail lumineux de ta part que je vais étudier les jours prochains.
Merci!
|
|
|
C'était pour rire, l'humour est délicat en général et en plus s'il y a seulement l'écrit.
Sur le fond, je trouve que cet article est quand même remarquable par son contenu, ce qui est l'essentiel.
|
|
|
Hommage à Mathusalem : le 16/09/2012 - 16:40
|
|
|
|



