|
| Finale de pions par Me***ry*12028 le
[Aller à la fin] |
| Finales | |
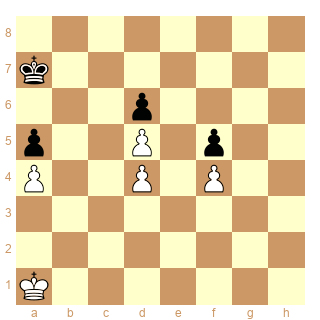
Dans cette position comment peut-on prévoir que Rb1 gagne tandis que Rb2 fait nulle?
En partie réelle, j'aurais plutôt tendance à me précipiter sur 1.Rb2
|
|
|
ce qui, peut être ne t'empêcherait pas de gagner :)
|
|
|
Vu comme ça évidemment En admettant que l'adversaire joue parfaitement, Rb2 fait nulle. Bien sûr s'il joue n'importe quoi il y a toujours moyen de gagner.
|
|
|
il faut partir de la position finale... rentrée du roi blanc en b5 ou en g5...
|
|
|
je plaisantais bref ...
Prévoir c'est calculer ... donc en reponse à ta question, comment prévoir ? bah y a qu'à calculer ... c'est tout :) ... sauf si tu pensais que tu jouais aux petits chevaux hihi
|
|
|
Aaaah des cases conjuguees! D'abord tu reperes les cases d'entree a surveiller c4/b6 et h4/g6 (meacae de rentrer en b5 ou g5 avec le roi blanc). Ensuite, tu definis les cases correspondantes c3/b7, d3/c7, c2/b8, d2/c8 c'est-a-dire la case que doit occuper le roi noir selon la position du roi blanc, afin d'eviter tout penetration (ou a l'inverse la position a atteindre trait aux noirs pour gagner avec les blancs). Enfin, tu tricotes autour de cette zone pour realiser que si le roi blanc va en a3, d1 ou a1 le roi noir doit repliquer par a7 ou c7. S'il va en b2 le roi noir devra jouer Rc8 (c1 et b7 etant conjuguees).
Ainsi, a linverse le roi noir etant en a7 le roi blanc doit occuper la case correpsondante b1, d1, b3 ou d3, d'ou 1.Rb1+-. Par exemple 1.Rb1 Rb7 2.Rc1 Rc7 3.Rd1 Rc8 4.Rd2 Rd8 4.Rc2 Rc8 5.Rd2 Rd7 6.Rc3 Rc7 7.Rd3 Rd7 8.Rc4 Rc7 9.Rb5 gagne
|
|
|
C'est moi qui peine ou c'est vachement difficile?
|
|
|
Puisque d3 et c7 sont conjuguées sur 4... Rd8 je jouerais plutôt 5 Rc3 Rc7 6 Rd3 etc.. La variante principale est donc bien 4...Rc8 5 Rd2! Rd7 6 Rc3!
|
|
|
La difficulté de ce genre de position... c'est de sentir d'instinct que les coups Rb1 et Rb2 ne sont pas équivalent ....
Et de se dire alors que cela vaut la peine de se fatiguer à calculer la difference entre les deux coups...
Il est impossible de calculer toutes les variantes possibles en permanence...
l'experience en finale est tres importante pour "sentir" cela....c'est pour cela que je conseille toujours aux debutants ( et aux autres aussi ) de jouer toutes les parties jusqu'au bout de la finale , car à force faire des parties nulles sans jouer la finale en se disant , c'est egal , on ne sait plus jouer les finales ni les "sentir"!
|
|
|
intéressant thierrycatalan ce que tu dis. Mais si on a le nez bouché ?
|
|
|
ah, les caes conjuguées.... pour les repérer, il faut repérer les cases les plus faciles...
soit d3 et c7 car si tu penses comme d'habitude à d3/d7 (opposition à distance)tu perds car sur Rc4, tu joues Rc7, le roi blanc rentre en b5 et tu perds...
et après, tu calcules... de l'autre côté, sur h4 pour rentrer en g5, la case conjuguée est g6, pour éviter le contournement... mais comme le dit thierrycatalan, le mieux, c'est l'expérience...
|
|
|
Il me paraît évident que cette position ne peut être gérée correctement que par le calcul, et non l'éxpérience (même si celle-ci permet de savoir ...qu'elle ne suffit plus et qu'il faut commencer à calculer.
Et là, dans cette position, en temps limité de partie, il faut être soit un supercalculateur soit un véritable spécialiste des finales de ce type, autrement dit avoir bossé les cases calculées pendant des heures et des heures.
Bref, personnellement, je la joue simplement , avec 1/Rb2, en misant sur une opposition ( pas trop éloignée) ,et je prie pour que mon adversaire soit aussi mauvais que moi...
|
|
|
C'est sur que je ne suis pas capable de calculer dans une position pareille.
Mais j'aurais peut-être jouer Rb1 en pensant: je reste sur les cases blanches étant donné que je les contrôle à l'aile dame et que les noirs ne les contrôle pas.
Ceci dit, je pourrais aussi me dire qu'il faut centraliser le + vite possible et jouer Rb2.
Ou alors suivre le conseil de Shereshevsky: ne pas jouer vite en finale et donc jouer Rb1
Ou alors............:o)
|
|
|
Tentative de réponse à la question de Mercury Le calcul et l'instinct c'est bien beau mais ça ne répond pas vraiment à la question posée par Mercury.
Et puis l'instinct n'étant rien d'autre que l'ensemble des réflexes acquis par l'expérience du jeu, il aurait justement plutôt tendance à faire jouer les coups considérés comme les plus "naturels" mais qui ne sont pas toujours les meilleurs.
En l'occurrence la plupart d'entre nous joueraient probablement 1.Rb2 histoire d'activer le Roi et non 1.Rb1!.
De la même manière, après 1.Rb2?, qui jouerait spontanément 1...Ra8!! pour annuler ?
C'est pourtant l'unique coup qui le permet, tous les autres offrant à nouveau le gain aux Blancs.
Quant au calcul brut, je souhaite bonne chance à ceux qui s'y hasarderaient ici : la ligne donnée ci-dessus par DrZen finissant par 9.Rb5 doit être une suite parmi quelques milliards de possibilités.
Dans le domaine des Finales, je crois au contraire que l'apprentissage de procédés techniques peut avantageusement éviter de se casser les dents sur ce genre de positions, en s'épargnant de laborieux et souvent vains calculs de variantes, tout en évitant aussi de se laisser piéger par son "instinct".
Et puis pourquoi ne pas profiter du travail des Anciens, histoire de gagner du temps ?
Evidemment cela demande parfois un peu de travail et la position proposée par Mercury n'est pas forcément la plus simple pour commencer à se familiariser avec les cases conjuguées, puisque c'est de cela qu'il s'agit.
Je vais donc essayer d'être un peu plus clair en détaillant la procédure.
"Repérer les Cases de Pénétration"
D'après ce que j'ai pu comprendre, dans le cas de finales de Pions complexes avec Pions bloqués, il faut tout d'abord repérer les cases de pénétration pour chaque camp, souvent assorties d'un gain de Pion.
Le Roi Blanc peut pénétrer par b5 et g5 alors que le Roi Noir ne peut pénétrer que par g4.
Cette simple constatation (2 cases de pénétration contre 1 seule) suffit pour conclure que seuls les Blancs ont des chances de gain, compte tenu de la position respective des Rois.
"Attention à la Contre-Attaque"
Dans les positions où la Défense dispose aussi d'une case de pénétration, il faut en revanche toujours garder à l'esprit que cela lui donne une possibilité de contre-attaque (ici à l'aile-Roi).
- Conséquence 1 : il faudra toujours vérifier que cette contre-attaque est trop longue pour aboutir; dans le cas contraire les Blancs devront soit l'empêcher (synonyme de partie nulle), soit laisser transposer dans une finale de Dames, en principe après avoir calculé qu'elle leur est avantageuse, mais alors ce n'est pas toujours évident
- Conséquence 2 : si les 2 Rois partent sur l'aile-Roi et s'y neutralisent, le Roi Blanc n'aura plus le temps de faire demi-tour vers l'aile-Dame à cause de cette contre-attaque.
Conclusion : Le Roi Blanc ne devra foncer sur l'aile-Roi que s'il est assuré de pénétrer en g5 et d'empocher le Pion f5.
Les Blancs doivent donc plutôt manoeuvrer initialement sur l'aile-Dame et se garder de s'approcher trop près de l'aile-Roi, c-à-d sur des cases où la contre-attaque Noire deviendrait possible.
Voilà pour quelques principes généraux.
Voyons maintenant plus concrètement comment procéder en pratique.
"Etablir les Positions de Zugzwang Réciproque"
Après avoir repéré les cases de pénétration du camp de l'attaque (= cases b5 et g5 pour le Roi Blanc), il faut établir les positions de zugzwang réciproque autour de ces cases, c-à-d les positions respectives des Rois autour de ces cases qui permettent effectivement soit au Roi Blanc de pénétrer au coup suivant si les Noirs ont le trait, soit au Roi Noir de défendre la case si les Blancs ont le trait.
- Pour la case b5, il s'agit de la position Roi Blanc en c4 et Roi Noir en b6
- Pour la case g5, il s'agit de la position Roi Blanc en h4 et Roi Noir en g6

En d'autres termes, les cases c4 et b6 sont conjuguées, ainsi que les cases h4 et g6.
Cela signifie que leur occupation simultanée par les Rois avec le trait à l'adversaire est synonyme de gain pour les Blancs (trait aux Noirs) ou de nulle pour les Noirs (trait aux Blancs)
"Etablir le Chemin le Plus Court"
Il faut ensuite établir le Chemin le plus court entre ces cases de zugzwang réciproque.
Pour les Blancs : c4-d3-e3(e2)-f3(f2)-g3-h4 (6 cases)
Pour les Noirs : b6-c7-d7(d8)-e7(e8)-f6(f7)-g6 (6 cases)
Quand le chemin du camp de l'Attaque est plus court que celui de la Défense, la victoire est en général facile.
Ici les chemins sont de même longueur (6 cases), ce qui implique la conjugaison entre les cases équidistantes de chaque extrémité du chemin.
C-à-d notamment conjugaison entre d3 et c7.
Je passe sur les conjugaisons suivantes car elles sont dégénérées (plusieurs cases sont possibles, par exemple d7 ou d8 en réponse à e3 ou e2), ce qui facilite en général la défense.
Sur le plan pratique il est néanmoins important de noter qu'il suffit au Roi Noir de se tenir 1 colonne vers la gauche par rapport au Roi Blanc pour arriver à temps pour défendre l'aile-Roi.
Mais si le Roi Noir se laisse distancer de 2 colonnes vers la gauche, alors le Roi Blanc pourra aller envahir l'aile-Roi.
"Recherche de Nouvelles Cases Conjuguées"
L'étape suivante consiste à établir de proche en proche de nouvelles paires de cases conjugués en recherchant de préférence v
- à établir des correspondances non dégénérées (en tout cas pour le camp de la Défense).
- à étendre le réseau de cases conjuguées le plus possible vers la zone où se trouvent les Rois afin de trouver le "bon" coup (quand il existe)
Pour trouver de nouvelles cases conjuguées, la méthode standard consiste à rechercher des cases contiguës communes aux cases déjà identifiées.
Par exemple dans le camp Blanc, c4 et d3 ont une seule case contiguë commune accessible au Roi Blanc : c3
Dans le camp Noir, b6 et c7 (les cases conjuguées de c4 et d3) ont une seule case contiguë commune accessible au Roi Noir : b7
Conclusion : c3 et b7 sont conjuguées
On remarquera aussi que ces cases respectent la "règle" du "décalage d'1 colonne" mentionnée plus haut.
En suivant le même raisonnement, on remarque que les cases c3 et d3 ont cette fois-ci 2 cases contiguës communes : c2 et d2.
Dans le camp des Noirs, les cases b7 et c7 (respectivement conjuguées de c3 et d3) ont aussi 2 cases contiguës communes : b8 et c8.
Mais attention, il faut se rappeler que le Roi Noir ne doit pas se laisser distancer de 2 colonnes vers la gauche sous peine de ne pas avoir le temps d'aller défendre l'aile-Roi.
Par conséquent, c8 est conjuguée avec d2, et donc b8 est conjuguée avec c2.
Récapitulons les cases conjuguées à l'aile-Dame :
1 = c4/b6
2 = d3/c7
3 = c3/b7
4 = d2/c8
5 = c2/b8
v
Pour mieux suivre, je conseille de s'aider d'un diagramme et d'y rajouter les chiffres indiqués sur les cases correspondantes.
"Zone de Conjugaison Principale"
L'ensemble des ces cases définissent en fait la zone de conjugaison principale.v
Remarque : cette conjugaison n'est relative qu'à la lutte pour la case de pénétration b5.
Les cases 1-2-3 sont disposées selon un Triangle car la case "1" est voisine de cases inaccessibles : b4 et d4 pour le Roi Blanc et c6 pour le Roi Noir.
La case "1" aura donc un statut un peu particulier dans ce système de conjugaison, hormis le fait qu'il s'agisse de la case ultime à atteindre (à l'aile-Dame).
Par ailleurs, les cases à l'arrière de la case "1" (cases 2-3-4-5) sont disposées selon un Carré.
On a par conséquent affaire à un système de conjugaison du type Triangle-Carré, ainsi répertorié par les théoriciens des cases conjuguées tels que Zinar.
"Report de numérotation - Zone de Conjugaison Secondaire "
On peut alors étendre la Zone de Conjugaison Principale pour constituer une Zone de Conjugaison Secondaire en bordure du Carré de la zone principale en utilisant une règle simple souvent employée et consistant à répéter la numérotation déjà établie dans le Carré en la reportant sur des cases situées à des distances correspondant à "l'opposition directe".
Pour être plus clair, on peut attribuer à b3 le chiffre "2", comme pour la case "mère" d3.
De même,
- b2 aura le chiffre "4" comme la case "mère" d2
- c1 aura le chiffre "3" comme la case "mère" c3
- d1 aura le chiffre "2" comme la case "mère" d3
- b1 aura le chiffre "2" comme la case "mère" d3 (opposition diagonale)
Remarques :
- certains auteurs préfèrent la nomenclature "2a", "3a", etc., pour distinguer les cases de la zone secondaire de celles de la zone principale.
- La conjugaison dans la zone secondaire se réfère toujours à la lutte pour la pénétration par la case b5
- une des raisons "géométriques" pour lesquelles ce procédé de report de numérotation toutes les 2 cases fonctionne à partir d'un carré est que les nouvelles cases (cases "filles") ainsi définies, sont toujours contiguës de cases portant les mêmes chiffres que les cases voisines de la case "mère" dans la zone principale.
Exemple :
- b2 (case "fille" "4", ou case "4a") est contiguë de cases numérotées "2" sur la même colonne ou numérotées "3" ou "5" sur la colonne voisine.
- la case d2 (case "mère" "4") a les mêmes propriétés.
Si on procède de manière similaire dans le camp des Noirs, on peut établir les cases conjuguées secondaires suivantes :
- a8 = (4)
- a7 = (2)
On pourra éventuellement étendre la zone secondaire Noire aux cases d7 et d8 :
- d7 = (3)
- d8 = (5)
On pourra alors remarquer que si le Roi Blanc est par exemple en b3 (case "2" de la zone secondaire, ou "2a") les Noirs se défendent aussi bien avec Rc7 (case "2" de la zone principale) qu'avec Ra7 (case "2" de la zone secondaire).
"Toujours préférer la Zone Principale à la Zone Secondaire"
Il convient pourtant de noter une règle essentielle : il est toujours préférable d'occuper la zone principale.
- Du point de vue de laDéfense on peut même ajouter que si le Roi Blanc est dans la zone principale, le Roi Noir doit obligatoirement occuper la case conjuguée de la zone principale et non une case conjuguée de la zone secondaire
Ainsi, si le Roi Blanc est en d3 (case "2" de la zone principale), seul Rc7 (case "2" de la zone principale) assure la nulle car en a7 (case "2" de la zone secondaire) le Roi Noir est trop décalé sur la gauche (3 colonnes).
De même, si le Roi Blanc est en c3 (case "3" de la zone principale), seul Rb7 (case "3" de la zone principale) assure la nulle car en d7 (case "3" de la zone secondaire) le Roi Noir est trop éloigné de la cruciale case "1".
- Du point de vue de l'Attaque, cette règle est également valable, et à la première occasion le Roi Blanc devra rentrer dans la zone principale avec la conjugaison ou alors en s'assurant que le Roi Noir ne peut pas la récupérer (voir plus loin la Règle du "Saut Opportun").
Récapitulons à nouveau les cases conjuguées à l'aile-Dame :
1 = c4 / b6
2 = d3(b1-b3-d1) / c7(a7)
3 = c3(c1) / b7(d7)
4 = d2(b2) / c8(a8)
5 = c2 / b8(d8)
Ce système de cases conjuguées permet déjà de trouver la solution de l'étude (sans avoir eu à calculer la moindre variante).
En effet, le Roi Noir se trouve en a7, c-à-d sur une case "2". Le Roi Blanc peut lui-même atteindre une seule case "2" : la case b1 (case "2a").
D'où la clé : 1.Rb1! et non 1.Rb2? (case "4a") sur quoi les Noirs annulent par 1...Ra8!! (case "4a") comme il est maintenant facile de le comprendre.
"Le Plan d'Attaque"
Après 1.Rb1! , les Blancs doivent conserver la conjugaison dans le système établi précédemment, en cherchant dans un premier temps à passer de la zone secondaire à la zone principale (= le Carré c3-d3-c2-d2), pour ensuite progresser dans le Carré (cases 5-4, puis 3-2), pour atteindre finalement la case ultime c4 (case "1").
Evidemment l'objectif secondaire des Blancs restera la pénétration par h4-g5 dès que le Roi Noir se décalera de 2 colonnes vers la gauche par rapport au Roi Blanc.
"Règle du Saut opportun"
Le passage de la zone secondaire à la zone principale puis la progression dans la zone principale ne sont pas toujours possibles en se contentant d'occuper les cases conjuguées de celles occupées par le Roi Noir.
Au contraire, on y parvient en général en "sautant" à la première occasion sur une case de la zone principale dont la case conjuguée n'est pas accessible au Roi Noir car trop éloignée de lui (le plus souvent à 2 cases, soit en opposition, soit à un saut de Cavalier).
Cette règle, dont la signification sera je l'espère mieux comprise dans l'exemple qui suit, est essentielle pour progresser dans tout système de cases conjuguées.
Elle équivaut, dans le système plus simple d'opposition directe autour de 3 cases-clés contiguës, à l'étape de contournement par le Roi autour de la case-clé centrale pour s'emparer d'une case-clé latérale (mais si cette allusion vous échappe, oubliez-la).
Examinons une suite possible pour expliciter ce qui précède (entre parenthèse figure le numéro de la case conjuguée) :
1.Rb1! ("2a") Rb7 ("3")
2.Rc1! ("3a") Rc7 ("2")
3.Rd1! ("2a")
Jusqu'ici le Roi Blanc s'est contenté de conserver la conjugaison dans la zone secondaire en longeant les cases "4" et "5" de la zone principale, faute de pouvoir s'y rendre sous peine de perdre la conjugaison.
Mais maintenant le Roi Noir a un choix difficile à faire :
1) sur 3...Rb6-b7-b8, le Roi Noir se décale de 2 colonnes à gauche et le Roi Blanc peut donc passer par l'aile-Roi
2) sur 3...Rc8 ("4"), le Roi Blanc joue 4.Rd2 ("4") et rentre dans la zone principale tout en conservant la conjugaison
3) sur 3... Rd8 ("5a"), le Roi Blanc joue 4.Rc2 ("5") et rentre dans la zone principale tout en conservant la conjugaison
4) sur 3...Rd7 ("3a"), les Blancs doivent jouer de façon plus subtile pour progresser en ayant recours à la "Règle du Saut Opportun".
Jouer 4.Rc1 ("3a") conserve en effet la conjugaison mais après 4...Rc7 ("2") on se trouve dans une impasse car les Blancs doivent à nouveau rejouer 5.Rd1 ("2a") pour conserver la conjugaison. Or en d7, on observe que le Roi Noir se trouve sur une case voisine des cases "2" et "4", mais surtout qu'il est à 2 pas des cases "3" et "5". De son côté, le Roi Blanc en d1 se trouve sur une case voisine des cases principales "4" (d2) et "5" (c2).
Pour progresser, le Roi Blanc doit donc saisir l'occasion de rentrer par c2 ("5") dans la zone principale car le Roi Noir n'a pas la possibilité d'occuper la case conjuguée b8 ("5") trop éloignée.
D'où la suite :
3...Rd7 ("3a")
4.Rc2! ("5" = case non conjuguée mais saut opportun !)
4...Rc8 ("4")
5.Rd2! ("4")
Après avoir pénétré dans la zone principale, le Roi Blanc a ensuite conservé la conjugaison.
Maintenant, comme au 3ème coup, le Roi Noir a des problèmes :
1) sur 5...Rb7-b8, il se décale de 2 colonnes à gauche et le Roi Blanc peut donc passer par l'aile-Roi
2) sur 5...Rc7 ("2"), le Roi Blanc joue 6.Rd3 ("2") et progresse dans la zone principale tout en conservant la conjugaison
3) sur 5... Rd7 ("3a"), le Roi Blanc joue 6.Rc3 ("3") et progresse dans la zone principale tout en conservant la conjugaison
4) sur 5...Rd8 ("5a"), on observe à nouveau que le Roi Noir se trouve sur une case voisine des cases "2" et "4", mais qu'il est à 2 pas des cases "3" et "5". De son côté, le Roi Blanc en d2 se trouve sur une case voisine des cases "2" (d2), "3" (c3) et "5" (c2).
Pour progresser vers la case ultime "1", le Roi Blanc doit non pas jouer 6.Rc2 ("5") qui conserve la conjugaison mais ne fait pas avancer le schmilblick, mais jouer 6.Rc3 ("3") car le Roi Noir n'a pas la possibilité d'occuper la case conjuguée b7 ("3") trop éloignée.
Une suite pourrait donc être :
5...Rd8 ("5a")
6.Rc3! ("3" = case non conjuguée mais saut opportun !)
6...Rc7 ("2")
7.Rd3! ("2")
7...b6 ("1") [7...Rb7 8.Re3! = attaque à l'Est]
8.Rc4 ("1") Zugzwang [ou 8.Re3= attaque à l'Est]
8...Ra6 (sinon le Pion a5 tombe)
9.Rd3! suivi de l'attaque à l'Est et c'est le Pion f5 qui tombe
Voilà pour l'explication du coup clé 1.Rb1! ainsi que de la manoeuvre complète de gain.
On voit que l'application de quelques règles simples permet en fait de venir à bout de cette finale hermétique au premier abord.
On peut aussi tirer d'autres enseignements de la position en analysant le jeu avec le trait aux Noirs.
Selon le réseau de cases conjuguées établi précédemment, il est facile de comprendre que les Noirs annulent avec 1...Rb7 ("3") ou 1...Rb8 ("5") car dès que le Roi Blanc passera sur la colonne b, il occupera une case "2a" ou "4a". Il suffira alors au Roi Noir de récupérer la conjugaison sur la colonne a par ...Ra7 ("2a") ou ...Ra8 ("4a").
En revanche 1...Rb6? ("1") offre le gain aux Blancs.
En effet ceux-ci doivent alors répondre non pas 2.Rb1? ("2a") à cause de 2...Ra7 ("2a") ou 2...Rc7 ("2"), mais 2.Rb2! ("4a"), car le Roi Noir n'a pas de véritable case "4" à sa disposition.
Une question se pose tout de même : qu'en est-il de la case a6 ?
Selon la "Règle du Report de Numérotation", a6 pourrait "presque" être numérotée "4a" puisqu'elle se trouve en bordure du Carré de la zone principale et en opposition diagonale directe avec la case "4" de ce Carré (case c8).
Cependant, même s'il est vrai que a6 partage certaines propriétés avec c8 (elles sont toutes deux voisines de cases "2" et "3"), elle présente aussi certaines particularités : par exemple contrairement à c8, elle est voisine de la case "1" (b6) mais pas de la case "5" (b8).
Et les cases "1" et "5", bien qu'étant distantes d'une opposition directe, ne sont pas totalement équivalentes. En effet, comme on l'a évoqué plus haut, la case "1" présente un statut particulier du fait qu'il s'agisse de la case ultime du système Triangle-Carré et qu'elle soit bordée de case(s) inaccessible(s) au Roi (ici la case c6).
Le Report de Numérotation n'est donc pas "fiable" sur la traverse de la case "1".
Ainsi, après 1...Rb6? ("1") 2.Rb2! ("4a") Ra6, les Blancs poursuivent 3.Rc2! ("5").
Pour éviter de donner la conjugaison, les Noirs doivent alors jouer 3...Rb6 ("1").
On constate alors que le Roi Noir ne peut pas sauter sur la case "4" du Carré (c8), et les Blancs jouent donc 4.Rd2! ("4"). Après quoi, faute de pouvoir aller en c6 (qui aurait fait une case "4a" idéale) les Noirs doivent jouer 4...Rc7 ("2") pour rester à 1 colonne du Roi Blanc.
Le Roi Blanc peut alors s'emparer de la conjugaison et l'emporter : 5.Rd3! ("2") zugzwang
Conclusion :
Cette finale est assez ardue, surtout si on n'a aucune expérience du monde des cases conjuguées.
J'espère cependant avoir pu éclairer un peu plus la lanterne de Mercury.
En tout cas j'ai essayé de fournir une "méthode" aussi détaillée que possible en faisant à la fois une synthèse de ce que j'ai pu lire mais aussi en essayant d'explorer les zones qui me paraissaient un peu obscures ou mal expliquées, voire pas du tout, quitte à créer mes propres "recettes", comme par exemple la Règle du "Saut opportun" qui me paraît incontournable pour la conduite de ces finales mais que je n'ai trouvée réellement explicitée nulle part, alors que pour les joueurs de mon niveau il me semble essentiel de formuler une telle règle.
Le résultat est un peu long, mais je crois que c'est le prix à payer pour avoir quelque chose de compréhensible par le plus grand nombre. Moyennant quoi, avec une lecture attentive on doit pouvoir arriver à comprendre le principe du raisonnement et ainsi appliquer la même démarche à d'autres positions similaires.
Tout commentaire, complément, correction, etc., est évidemment le bien venu pour améliorer cette "méthode".
Bien sûr, je crois qu'une étude plus complète des différents systèmes de cases conjuguées et s'appuyant sur le travail théorique accumulé depuis plus d'un siècle à partir de ce type de finales de Pions bloqués doit suffire à acquérir une connaissance plus globale et à se forger une technique permettant de venir à bout de la plupart de ces positions.
Je renverrais en particulier au travail de systématisation de Zinar qu'on retrouve dans le Compehensive Chess Endings d'Averbakh. On peut également tirer profit du Secrets of Pawn Endings de Müller et Lamprecht, bien que moins complet, ainsi que du Finales de Pions de Maizelis, malgré pas mal d'erreurs de traduction et de sources de confusions dans la présentation.
Pour finir, je rappelle que la position initiale est attribuée à Reichhelm (Chicago Tribune, 1901) et correspondrait à une amélioration d'une étude de Lasker qui avait placé les Rois en a3 et a8 (Manchester Evening News, 1901) , dixit Maizelis qui aurait interrogé Lasker lui-même à ce sujet en 1973.
Je vous laisse trouver la solution de l'étude de Lasker.
|
|
|
Félicitations à Kloch pour ce travail précis et très complet, que je viens de survoler.
Devant l'apparente difficulté extrême de la procédure, une question naturelle me vient à l'esprit : combien de temps , à peu près ,faut-il pour "résoudre" une position de ce type, quand on connaît le système des cases conjuguées aussi bien que toi ?
En clair, est-ce applicable à une partie de compétition à la pendule ?
|
|
|
Oui. Honnêtement, je pense qu'il faut moins d'un quart pour être certain que Rb1 gagne et b2 fait nulle.
LA grosse difficulté, c'est de se rendre compte du problème et de pas jouer Rb2 a tempo en ce disant "je verrai bien avec mon roi centralisé" !
|
|
|
d'un quart d'heure Quand pourra-t-on éditer ses messages sur france-echecs ?
|
|
|
Pour ma part Je ne vois pas en quoi h4 et g6 sont conjuguées. Si le trait est aux noirs et qu'ils jouent Rh6, que se passe-t-il ?
|
|
|
Sur ...Rh6 le Roi blanc parvient en b5.
|
|
|
@ Cyrillev : ta remarque est intéressante et me permet de clarifier une confusion assez courante sur ce que signifie la conjugaison.
Obtenir la conjugaison n'est pas une fin en soi et ne garantit pas le gain quelles que soient les circonstances.
La conjugaison est seulement un moyen garantissant de pouvoir atteindre certaines cases-clés, ici les cases critiques des Pions Noirs a5 et f5 (respectivement b5 et g5) dont l'occupation par le Roi Blanc conduit au gain du Pion correspondant.
Les cases h4 et g6 sont donc conjuguées compte tenu de l'objectif du camp de l'attaque (les Blancs) qui est de pénétrer par b5 ou g5.
Cela signifie qu'après ...Rh6, le Roi Blanc peut bel et bien repartir vers l'aile-Dame et pénétrer par b5 pour gagner le Pion Noir a5.
En revanche, comme je le soulignais aussi très tôt dans mon (long) exposé (paragraphe "Attention à la Contre-Attaque"), les Noirs disposent eux-aussi d'une case de pénétration à l'aile-Roi (g4), et ils auront alors la possibilité de contre-attaquer sur l'aile-Roi pour gagner le Pion Blanc f4. Ce qui oblige le Roi Blanc à rester sur l'aile-Roi. La position est alors nulle.
Comme souvent aux échecs, il faut donc tenir compte également de toutes les caractéristiques de la position, parmi lesquelles les possibilités de pénétration du camp de la défense sont un élément essentiel.
Il en résulte que dans la position initiale avec les Rois à l'aile-Dame, les Blancs doivent avoir comme premier objectif de menacer de pénétrer par b5 (d'où la recherche du réseau de cases conjuguées autour de c4 et b6) et ne doivent se diriger en seconde intention vers l'aile-Roi que s'ils ont l'assurance d'empocher le Pion f5, c-à-d si le Roi Noir s'est décalé de 2 colonnes à gauche par rapport au Roi Blanc.
|
|
|
Vache, félicitation Kloch, et tout ca sans possibilité de rééditer son message, standing ovation !
|
|
|
Euh ... tu as quand même écrit ça : En d'autres termes, les cases c4 et b6 sont conjuguées, ainsi que les cases h4 et g6.
Cela signifie que leur occupation simultanée par les Rois avec le trait à l'adversaire est synonyme de gain pour les Blancs (trait aux Noirs) ou de nulle pour les Noirs (trait aux Blancs).
Ce n'est pas moi qui l'ai inventé ;-). Donc il n'y a en effet pas de zugzwang réciproque en h4/g6 -ni même de zugzwang tout court. En revanche, en c4/b6 c'est bien le cas.
|
|
|
Ah oui pour l'édition aussi, bravo. Là déjà, j'ai voulu mettre < p > et ça n'a pas marché. J'en conclus que c'est < br > mais je n'irai pas bien loin ... alors que là c'est une démonstration -et pas seulement sur la forme.
|
|
|
Bien vu Cyrillev J'ai en effet fauté, mais c'est dur de rester concentré entre 2 et 3 heures du mat.
Je propose la correction suivante :
"Cela signifie que leur occupation simultanée par les Rois avec le trait à l'adversaire est synonyme de gain d'un Pion pour les Blancs (trait aux Noirs) ou de nulle pour les Noirs (trait aux Blancs)."
Par conséquent, et comme je l'explique dans mon précédent message, je maintiens le fait que dans le cadre formel du réseau de cases conjuguées établi il y a bien zugzwang réciproque en h4/g6, c-à-d si l'on s'en tient à la lutte globale pour les points de pénétration en b5 ou g5 par le Roi Blanc :
- trait aux Blancs = le Roi Blanc ne passe pas
- trait aux Noirs = le Roi Blanc passe, même si c'est en b5 et qu'en pratique il ne peut se le permettre à cause de la contre-attaque Noire
|
|
|
à Kloch je répète ma question :
Combien de temps de réflexion estimes -tu nécessaire pour la résolution d'un tel problème en partie à la pendule (en compétition) ?
J'ai bien noté la réponse de Puch :moins d'un 1/4 d'Heure
|
|
|
Merci Kloch Il faudra que j'étudie ça de près quand j'aurai le temps. Tu as dû établir le record de la réponse la plus longue. Ca confirme ce que je pensais: c'est compliquée comme position.
|
|
|
Felicitation Kloch !! Excellent expose. De plus tu fais un gros effort pour t'abaisser au niveau de quelqu'un qui ne maitrise pas ce theme.
Je ne resiste pas a l'envie de vous recommander ce probleme qui ressemble un peu a celui du diagramme (pas peu fier le gars !).
Supergogol: Avec un papier et un crayon, moins d'une minute, et en etant sur de moi a 100%. Dans les conditions d'une partie, 10 min pour trouver Rb1, et 10 de plus pour etre sur de moi.
|
|
|
@ supergogol : temps de réflexion nécessaire Il m'est un peu difficile de répondre mais l'un dans l'autre, moins d'1/4 d'heure me semble en effet raisonnable, voire moins quand il s'agit d'appliquer une méthode bien rôdée sur une position moins complexe.
En fait, moins d'1/4 d'heure peut paraître vraiment court pour ceux qui découvrent ces notions de cases conjuguées, surtout si on songe qu'il a fallu attendre le 20e siècle pour commencer à les rationaliser. Mais justement, le travail a maintenant déjà été mâché en grande partie par d'autres et il "suffit" donc de s'appuyer dessus.
Comme pour toute technique, le plus gros du boulot doit se faire non pas pendant la partie mais en amont en étudiant les procédés adéquats et surtout en les assimilant suffisamment bien pour savoir quand et comment les appliquer.
Par conséquent, en partie réelle, le temps de réflexion nécessaire va surtout dépendre du degré de similitude entre la position sur l'échiquier et celles que tu as déjà étudiées et assimilées.
Bien sûr, d'autres considérations plus triviales qui affectent la capacité de concentration vont aussi intervenir : pression de la pendule, durée de la partie déjà écoulée et efforts déjà consentis, qualité de la digestion du repas précédent et du sommeil de la dernière nuit, etc.
Mais plus sérieusement, je crois aussi que de manière générale les positions ne surgissent pas du néant sur l'échiquier comme c'est un peu le cas quand on ouvre un bouquin d'échecs ou qu'on se retrouve sur un forum face à une position qu'on découvre de but en blanc. Je veux dire par là qu'au cours d'une partie réelle, le bagage technique et toutes les connaissances acquises permettent en fait au joueur d'orienter plus ou moins consciemment la partie vers des positions avec lesquelles il se sentira le plus à l'aise.
En d'autres termes tu auras plus de chance d'avoir à affronter ce genre de situations si tu t'en sens capable a priori, car tu peux avoir le choix de parvenir ou non à ce type de positions là. Ce qui biaise d'ailleurs un peu ta question car il est alors probable que tu ailles même jusqu'à anticiper la position en cherchant à la résoudre avant de la provoquer sur l'échiquier.
Ceci dit, je n'ai personnellement jamais eu à calculer des finales avec Pions bloqués basées sur des réseaux complexes de cases conjuguées. Mais il est vrai que je joue assez peu en compétition, ce qui ne m'empêche d'ailleurs pas de prendre du plaisir à étudier la technique des finales, sans doute à cause de mon esprit "scientifique".
|
|
|
@ CapitaineFlam "De plus tu fais un gros effort pour t'abaisser au niveau de quelqu'un qui ne maitrise pas ce theme."
C'est sans doute parce que j'ai d'abord dû compléter les méthodes publiées pour les abaisser à mon propre niveau afin de les rendre applicables de façon plus carrée, en tout cas à mes yeux
... mais j'ai certainement encore dû oublier certains détails
|
|
|
excellent Kloch ! j'avais repérer les cases de pénétratins, les ases finales conjuguées mais je n'avais pas tout calculé...
je vais te lire tranquillement... MERCI ENCORE
|
|
|
, merci , Kloch pour cette réponse ,claire, et complète.
Etbravo pour ta démonstration, que je vais me faire un devoir d'étudier , à tête reposée...
|
|
|
Comme diraient les jeunes: "Trop balèze Kloch!"
ça a l'air passionnant, mais faut pas être feignant!!!
|
|
|
J'ai fait le test sur la position du capitaine Flam Bon, c'est un problème nettement plus facile, et j'étais déjà 'prévenu' qu'il s'agissait d'un pb de cases conjuguées, mais il m'a fallu dix secondes pour comprendre que 1.Rb1 est le seul coup intéressant (:p) et environ trois minutes télé allumée pour être absolument sûr du gain grâce à un passage sur la case f1.
|
|
|
Merci à m'sieur Kloch.
|
|
|
Pour ma part je trouve la position de CapitaineFlam bien plus compliquée à résoudre que celle de Lasker/Reichhelm, notamment à cause des Pions mobiles qui obligent à tenir compte de pas mal de paramètres supplémentaires dans le calcul préliminaire ou celui de vérification : effet des temps de réserve, possibilités de verrouillage de l'aile Roi, et autres subtilités tactiques comme ici la possibilité d'auto-pat du Roi Noir, ce qui explique la double finesse 5.Rf2! (au lieu de l'immédiat 5.Rf1? h5!) et 6.Rf1! (au lieu de 6.Rg2? Rd8!).
Bref, je trouve la méthode de résolution de ces possitions là bien moins facile à systématiser que celle avec Pions bloqués.
|
|
|
Très bel exposé ! Bravo à Kloch.
|
|
|
mouais, encore un profil vide.. je plaisaaaante..
Tres bel exposé en effet.
Je suis quand meme curieux de savoir qui est Kloch!
|
|
|
zkwxry mais un contresens dans la définition de l'instinct. Je suppose kloch que tu avais à l'esprit intuition mais tu ne peux donc pas reprocher aux autre de se tromper.
Peut-être avaient-ils à l'esprit une approche plus poétique voire provocatrice de la réalité échiquéenne. Va savoir
|
|
|
pour ta question Mercury par le calcul des oppositions royales sur les cases critiques
Toutes ces finales de pions bloqués sont, à ma connaissance, virtuellement théoriques et exige donc un calcul très précis si le résultat semble incertain.
Je te conseille d'avoir une approche concrète et de t'amuser à résoudre qq études. Analyser Rb2 te semblera alors naturel
|
|
|
et même Rb1 ; )
|
|
|
L'explication de Kloch .. .. est très bonne pour ce que j'en ai lu du moins.
Mais l'exemple de départ est un peu trop compliqué.
Aussi pour comprendre un peu mieux ce mystère des cases conjuguées en partant d'un exemple de base je vous conseille un article en deux parties de Karsten Müller dans sa rubrique Endgame Corner de l'excellent site ChessCafe.
Seul souci : c'est en anglais !
Partie1
Partie2
|
|
|
Pour moi non plus Mercury ça me parait pas évident a 1ere vue car je vois rapidement que l'on pourra jamais rentrer en b5 donc je me dis faut passer par l'autre coté (par exemple g5), et pour y arriver je peux y aller en zig zag ou tout droit bref meme par l'autre coté je vois pas comment rentrer lol
bon je regarderais ca mais ptet que ca parait evident pour ceux qui ont l'habitude de travailler ca ? ou les zugzwang
|
|
|
ah ok je vois c'est possible, mais bon y'a tellement de possibilités c'est vrai que de la a voir que des le 1er coup on peut se couper l'herbe sous les pattes ...dur ....
|
|
|
Astuces pratiques ;) Dans ce genre de finales, où les coups de Rois incroyables abondent, il faut bluffer!
Rb2 est trop normal, l'adversaire ne sentira pas votre (fausse) maîtrise. Donc jouer très lentement Rb1, avec un regard à la James Dean qui toise l'adversaire. Puis se lever sûr de soi, genre c'est gagné.
Puis prier que ca gagne...et éviter l'analyse post-mortem.
|
|
|
Tête reposée
Dr Zen, puis Kloch en détail, ont fait en sorte que tous les francéchéphiles soient en mesure de définitivement comprendre les cases conjuguées (ou "semi-conjuguées" comme h4/g6).
Parmi tous ceux (j'en ai dénombré quelques-uns) qui ont félicité et remercié Kloch, à juste titre, pour le soin qu'il a apporté à l'élucidation de l'étude Lasker/Reichhelm (en facilitant la tâche par des remarques telles que "le RN doit être une colonne à gauche du RB"), annonçant qu'ils allaient lire attentivement et méditer son texte à la première occasion, je serais curieux de savoir combien l'ont effectivement lu et, désolé d'insister, effectivement retenu. En d'autres termes, combien de ces attentifs promeneurs seraient capables, au besoin après un rafraîchissement de mémoire d'une trentaine de minutes, de l'exposer à l'échiquier mural de leur cercle.
Je projette une autre tentative sur un article semblable (ouvert par Kaktus, quoique je n'aie pas besoin du symbolisme de son pseudonyme pour poser les questions qui piquent), à propos d'une étude d'Ebersz, d'un aspect différent de celle-ci en ce sens que les pions sont immobilisés mais non bloqués.
|
|
|
Je viens de découvrir ce vieux topic (merci google) et l'explication de Kloch (merci Kloch) après la réalisation d'une animation en couleur pour cette même étude qui se trouve dans le livre "Comment jouer les fins de parties"
http://www.cpe95.org/spip.php?article838
c'est un PGN avec flèches et cases en couleur (avec chessbase)
mais je vais relire tout cela car l'identification des cases conjugués reste délicat
leur utilisation est simple SI on a réussit à les trouver
|
|
|
Quelqu'un sait-il si des matheux ont abordé ces questions ? Cela me paraît flirter avec la théorie des graphes, ou quelque chose de ce genre.
|
|
|
... élément de réponse (comme on dit au journal télévisé) : voir ce fil (http://www.france-echecs.com/article.php?art=20120829074120836), le 30/08/2012 - 00:22:14 et le 02/09/2012 - 20:06:41
|
|
|
Merci Kloch
|
|
|



