|
| Probleme mathematique par ins2417 le
[Aller à la fin] |
| Problèmes | |
Combien de chemins existent-ils pour un roi de passer de a1 jusqu'a h8 dans n coups exactement?
(C'est une variante d'une composition que j'ai propose pour le concours de compositions echecs-maths de Bonsdorff il y 18 mois.)
|
|
|
En fait, ça dépend ... De la position des autres pièces ...
Plus sérieusement, ce problème me semble plus être un problème d'algorythmie que de maths. Me trompe-je ?
|
|
|
reponse salut m. le capitaine,
on suppose que le roi est la seule piece sure l'echequier.
on cherche une formule "closed", avec les operateurs +,-,*,/,^, et pour la rendre plus court, on admet aussi le fonction "round" pour trouver le nombre entier plus pres.
alors si c'est une probleme mathematique.
|
|
|
Interesting! Déjà j'ai les réponses pour 0
|
|
|
balises j'ai les réponses pour n entre 0 et 7 inclus, c'est un premier pas! :).
|
|
|
Je chercherai! f({0...6})=0
f(7)=1
f(8)=2*(7*8/2)=56
...
La même question pour aller de a1 à a8, ou même pour aller de e1 à e8, a son intéret aussi.
|
|
|
Tiens le forum n'aime pas les accolades...
|
|
|
des acolades ces infos vont etre utils pour verifier la formule, que va etre quelquechose du genre f(n) = blahblah(n). Tu va pouvoir verifier que par exemple blahblah(0) est bien 0.
L'interet a mon avis c'est comment regarder la geometrie, pour que la solution blahblah apparait.
|
|
|
Le roi peut-il passer passer plusieurs fois par h8 (avant le dernier coup) ?
|
|
|
Pas la méthode dite du calcul brutal Je dirais f(9)=1305
|
|
|
ca sent les maths à haute dose sur ce post...Y a pas un prof qui a la solution ?
|
|
|
Mouais... Pt'et tenter une relation de récurrence sur f(n), f(n+1), f(n+2) ...etc pour n>=7, sachant que f(7)=1, f(8)=2x7=14 ...etc, mais ça me semble bien trop tordu pour essayer de répondre (à mon nivo en tt k) en 15 min passk'au delà de n=9 ou 10 y'a des trucs bizarres. Un gentil prof dans les parages? :-)
|
|
|
Hum Nous avons un f(8)=14 et un f(8)=56, c'est le second qui a ma préférence !
|
|
|
Mais que fait Nicolas ?? Ils hibernent encore à Lille ?? ;o)
|
|
|
Je suis en train de composer le premier prix retro a Messigny !
Et puis je vais te dire un truc, Claude, Andrew a ete medaille aux olympiades de maths. Alors quand il propose de trouver une formule, tu peux etre certain que c'est hyper-coton a decouvrir...
Cela dit, je retiens la question pour plus tard.
|
|
|
Encore une variante: Et pour aller de a1 à a1 en n coups, combien de possibilités ?
Promis, je me mets à chercher au lieu de vouloir encore compliquer...
Juste un point, Andrew: as-tu trouvé la solution, ou la question reste-t-elle complètement ouverte?
|
|
|
Generalisation Pour aller, sur un echiquier de taille infinie, d'un point a un autre en n coups, combien de possibilites ?
Si je dis pas de betise, cette fonction ne depend que de la distance entre les 2 points (et aussi de n bien sur).
|
|
|
généralisation ? Ben a priori cette généralisation est plus facile que le problème original puisqu'avec un échiquier infini il n'y a pas d'"effets de bord".
|
|
|
Si, la ballade sur échiquier est limitée à l'ensemble des points accessibles en n coups à partir de a sur un plateau infini. Donc on est ramené à un grand échiquier fini: (2n+1)x(2n+1) (sauf erreur de ma part). Mais bon... Je n'ai toujours pas d'idées pour résoudre ça :-/
|
|
|
J'écris un peu trop vite moi ;o) Dsl! En effet a priori pas d'effets de bords (et il ne s'en aperçoit qu'en se relisant... Pas doué le Benji).
|
|
|
Comment je modéliserais ça : A mon avis, le mieux est d'étudier séprément les mouvements verticaux et horizontaux du roi. Le problème devient :
Le roi va de la case de coordonnées (0,0) à la case de coordonnées (7,7).
A chaque coup, il passe de la colonne m à la colonne m-1, m ou m+1.
A chaque coup, il passe de la ligne p à la ligne p-1, p ou p+1.
Après, ce serait de la combinatoire simple s'il n'y avait les conditions suivantes :
Le roi ne peut pas jouer de (m,p) à (m,p) [où l'on voit que le mouvement du roi n'est pas si simple que ça !]
A chaque coup, on doit avoir m et p entre 0 et 7 (effets de bord).
Si vous voulez mon avis, c'est faisable (pour anselan !), mais c'est difficile (poiur moi !)
|
|
|
C'est la piste que je suivais cette nuit...
On en tire ce premier résultat très simple vis à vis du problème général:
Pour aller de a1 à h8 en n coups [n pris entre 7 et 14] sans revenir vers la gauche ni descendre vers le bas (i.e. tous les coups pris dans l'ensemble ((Z/2Z)²)* = [(0,1), (1,1), (1,0)]),
il y a C(n,7)*C(7,n-7) = 14!/((14-n)!*(n-7)!*(n-7)!) possibilités.
Mais cela est très dur à généraliser avec des coups dans ((Z/3Z)²)* [le problème initial] à cause des effets de bords notamment. Je pense qu'il va falloir mettre en place une autre stratégie de dénombrement pour que cela ne devienne pas trop fastidieux!
Pùch, vive les maths à une heure du matin avec 38.5 de fièvre!
|
|
|
Bon Histoire de faire le malin :
Je crois que f(10)=226 170
et ça ne m'aide pas du tout à généraliser !
|
|
|
C'est sans doute vrai que la variante que je propose (sans effet de bord) est plus facile que sur un echiquier borne. Mais c'est aussi plus interessant d'un point de vue mathematique, car plus permeable a l'utilisation de la geometrie.
|
|
|
Il y a un truc pour ignorer le bord. Mais faut deux autres trucs avant ca. :-)
|
|
|
Un indice ?
|
|
|
question: le roi ne peut pas retourner sur une case qu'il a déjà occupé?!
sinon c'est impossible à résoudre...
juste un ptite remarque en passant: f est définie sur [0,50] car après la règle des 50 coups met fin à la partie....
ok je sors
|
|
|
Mais si Jo' ! Et par Dead Reckoning, personne ne pouvant être maté, aucun coup ne peut être joué, et donc pour tout n, f(n)=0.
C'était si simple... Ah là là quel plaisantin cet Andrew, je le savais pourtant que c'était un spécialiste du DR mais je me suis quand même laissé avoir, ah là là...
|
|
|
Ref petiteglise Pourquoi le roi ne pourrait-il pas retourner sur une case qu'il a déjà occupée ?
A mon avis, il le peut sans problème...
|
|
|
ok, il peut y retourner deux fois mais pas trois sinon c'est nulle par répétition...
j'étais pas déjà sorti moi?
|
|
|
enfin non il peut y retourner 1 seule fois en fait
|
|
|
Ah oui Notons aussi qu'avec un seul sur l'échiquier, le camp adverse n'a aucun coup légal à sa disposition sans être en échec. Il y a donc pat.
Hum, bon je sors à mon tour, tu peux rentrer petiteglise.
|
|
|
mdr!!!
|
|
|
non non La position est illégale car il n'y a pas de roi noir. Il faut donc rajouter les pièces manquantes pour rendre la position légale, c'est à dire le roi noir.
Et dès lors si le roi blanc est en a1, où que l'on place le roi noir, celui-ci pourra empêcher les blancs d'atteindre h8. La réponse est donc f(n)=0, sauf en aidé. Ok je sors :).
|
|
|
responses varies D'abord il y a ni DR ni AR. Il n'y a pas de roi noir donc on ne considere pas un jeu. Il n'y a pas de regle de 50 coups, et pas de regle de repetition. Le roi peut revenir sur un case autant de foi qu'il veut.
Deuxieme chose. Nicolas a propose qu'on oublie le bord, qu'on balade dans une espace infinie. il est interessant a consider cette possibilite. Mais je crois que c'est plus facile a considerer l'echequier fini d'abord.
Troisieme chose. On me demande une indice. Je dirai que quelqu'un a deja suggere ici le premier etape a suivre.
Amities, Andrew
|
|
|
gah pourquoi le html ne marche plus ici?
|
|
|
euh... Le roi peut revenir sur un case autant de foi qu'il veut
Cela n'est-il pas une porte ouverte à une infinité de solutions ou est-ce le retour de l'hyperjeu? ;o)
|
|
|
dcax, tu es tombé dans le même "piège" que moi... relis l'énoncé!
|
|
|
'Faut être sacrement vicieux... pour proposer un problème pareil!
Etant pas trop expert es mathématiques, je me suis simplifié le problème, désignant la case b2 comme case d'arrivée et travaillant sur un échiquier délimité par ses 64 cases.
Ben rien que ça, je suis largué dès que ça se complique!
Bon, en 1 coup, il n'y a qu'une possibilité... a1 -> b2 lol
En 2 coups, c pas trop dur non plus, on passe par a2 ou b2, donc 2 solutions.
Mes neurones travaillent déjà à 99% quand je passe à 3 coups! J'imagine aisément 3 possibilités qui font un aller-retour par la case départ, plus 7 autres possibilités d'aller-retour si je vais sur b2 au premier coup. Ca fait déjà 10.
Ensuite je passe à n=4 et là... je peux trouver les 6 solutions qui font un aller-retour via la case départ.
a1-a2-a1-a2-b2
a1-a2-a1-b1-b2
a1-b1-a1-b1-b2
a1-b1-a1-a2-b2
a1-b2-a1-a2-b2
a1-b2-a1-b1-b2
Puis si je vais directement de a1 à b2, il me reste 7 cases à explorer (a1 c fait), chacune donnant 4 possibilités pour passer par une autre case avant de revenir à b2. Exemple: a1-b2-b3 et je peux passer par a2, a3, c2 ou c3 avant d'aller en b2.
Ca donne jamais que 34 possibilités...
J'ai même pas la force de penser à essayer n=5, ou encore d'éloigner la case sur c3 au lieu de b2!
Franchement je me demande comment on peut arriver à pondre une formule pour résoudre ce casse-tête...
|
|
|
Andrew a plus d'un tour dans son sac, tu peux me croire...
|
|
|
Cela etant dit, la formule qui m'interesse est celle sans bord, mais j'ai pas le temps en ce moment de chercher cette fonction de 2 variables f(n,d) qui, je pense, devrait avoir une belle gueule...
Tu la connais, Andrew ?
|
|
|
bande de malades ;o)
|
|
|
bon d'après ma formule f(7)=1 f(8)=56, f(9)=1309, f(10)=20370, f(11)=255366, f(12)=2782296;
J'ai une démonstration mais elle ne tient pas dans la marge de ce post.
|
|
|
Ca m'a l'air trop compliqué! Moi j'ai pas trop envie de chercher mais j'aimerais bien quand même avoir la solution!
Est ce qu'on l'aura en fin de post la soluce??
|
|
|
ref chascal : pour un échiquier de taille 2x2 ... c'est simple f(1)=1 et f(n+1) = 3f(n)-1 si n impair et f(n+1) = 3f(n)+1 si n pair. La suite des f(n) est donc 1, 2, 7, 20, 61 ...
|
|
|
Faut suivre l'indice que je vous ai donne.
|
|
|
est ce que dan a trouvé?
|
|
|
helas non car j'ai perdu la démonstration dans mes papiers :) J'ai juste écrit l'algorithme, donc trouvé comment le calculer (ce qui est facile), mais pas trouvé de formule.
|
|
|
c'est un peu du style théorème de Fermat cette affaire. La démonstration est écrite dans la marge d'un bouquin dont on ne trouve nulle part la trace!
|
|
|
Je crois bien que c'était là le clin d'oeil de Dan...
|
|
|
Argh La majorité se dessine pour f(8)=56, dan et moi sommes "presque" d'accord pour f(9), 1305 ou 1309, allez, on ne marchande pas, par contre, ça se corse pour f(10) ! Tu peux nous donner une idée de ton algorithme, dan ?
|
|
|
Si son algo est juste, et il n'y a pas de raison d'en douter, on peut féliciter Pessoa pour son excellent dénombrement de f(9), avec une micro-erreur de calcul de... 4!
Il a même eu le tact de très largement surestimer f(10) pour de pas pouvoir trop frimer quand même!
Je me suivi vaguement mis à la recherche d'un équivalent pour f(n)/f(n-1), pour n grand, mais cela est plus ardu que je ne l'espèrais... Après les partiels!
P~cheRo2+F
PS Andrew: merci, indice bien noté!
|
|
|
allez puch ... ... puisque l'algorithmie a eu raison des maths je te dirais que f(n)/f(n-1) a un équivalent simple puisqu'il tend vers une constante qui est 7.2909.
Quant à mon algo, ya pas plus simple, ca prend 10 lignes à programmer en Matlab, je te le donne avec plaisir cher pessoa :
- on crée un échiquier 10x10 (en fait un tableau d'entiers) où les cases de l'échiquier classique 8x8 sont bordés par une ligne ou colonne de chaque côté pour absorber les effets de bord.
- on initialise ce tableau avec des valeurs 0 partout sauf des valeurs 1 aux cases correspondant à h7,g8 et g7 : ceci signifie qu'à partir de ces 3 cases, on peut joindre h8 en 1 coup par 1 chemin (le 1 du tableau correspond au nb de chemins différents, pas au nb de coups), mais qu'il n'y a pas de tel chemin en 1 coup à partir des autres cases.
- Boucle principale : pour n allant de 2 à N, le tableau dans une case donnée x (noté t(x,n)) est tel que t(x,n)=somme (t(xi,n-1)) pour tous les xi voisins de x pour la marche du roi. L'astuce est que les lignes et colonnes bordantes de l'échiquier 10x10 ne sont pas mises à jour ici, seules les 64 cases de l'échiquier réel le sont.
A l'étape n, on a
|
|
|
... ... j'ai été coupé
A l'étape n, on a plus que ce que demande anselan, puisqu'on a l'information demandée pour toutes les cases de départ possible et pas seulement pour a1.
|
|
|
la signification ... ...de la boucle principale de l'algo est que le nombre de chemins pour aller par exemple de e4 en h8 en 10 coups, est le même que la somme du nombre de chemins pour aller des cases voisines de e4 (cad d3,e3,f3,d4,f4,d5,e5,f5)jusqu'en h8 en 9 coups.
|
|
|
on avance bon on a du logiciel qui peut se dire pour un tel n combien de chemins existent. ca peut s'aider a confirmer que la formule arithmatique que je demande est correcte. mais c'est quoi la formule?
|
|
|
je promets d'essayer anselan, mais je n'ai pas du tout de temps pour l'instant. Alors que l'algo m'a pris 5 minutes.
|
|
|
l'algorithme de dan31 donne... f(7)=1
f(8)=56
f(9)=1306
f(10)=20196
f(11)=251074
f(12)=2711584
etc...
Ca peut donner des idées (ou des possibilités de vérification) à ceux qui cherchent la formule d'anselan.
|
|
|
c'est bizarre mathou .... parce que j'ai ca (voir plus haut) : c'est presque la même chose mais bon pas exactement. f(7)=1 f(8)=56, f(9)=1309, f(10)=20370, f(11)=255366, f(12)=2782296;
De plus j'ai une vérification à la main (en dénombrant les différents cas) pour f(9)=1309
|
|
|
Oui, mais j'ai programmé ton algorithme en supposant.... ..que l'on s'arrête dès qu'on a atteint h8.
Si on va de a1 à h8 en 9 coups, par exemple, on s'arrête là, et on ne continue pas à se balader pour revenir en h8 au 12ème coup par exemple.
Si on ne fait pas cette supposition, on obtient les chiffres que tu viens de citer.
|
|
|
Il faudrait pu-être demander à anselan... ...si, dans son problème, le Roi s'arrête dès qu'il a atteint son but (h8) ou s'il peut continuer à se promener.
|
|
|
il peut continuer
|
|
|
Je pense qu'il faut demander à anselan... ...car il écrit : "...pour un roi de passer de a1 jusqu'a h8 dans n coups exactement"
On peut comprendre cela en pensant que si, par exemple, il arrive en h8 en 10 coups exactement, c'est qu'il n'y est pas arrivé en 7, donc qu'il n'est pas pas déjà passé auparavant par la case h8.
Dans cette interprétation, le but h8 aurait un statut particulier.
Le mieux est qu'il nous dise comment il faut comprendre son énoncé.
|
|
|
pour repondre (1) a dan: je voudrais simplement clarifier au gens ce que c'est le but. je ne voulais pas minimizer ce que tu as fait. pardon!
(2) le roi peut continuer a ballader apres avoir arriver a h8 le premier fois. mais au fin du n-ieme coup il doit etre a h8.
|
|
|
ref anselan pas de problème, ne t'en fais pas !!
Je suis le premier à minimiser ce que j'ai fait puisqu'il est bien plus intéressant de trouver une formule analytique à mon sens. J'avoue que pour le problème de Nicolas Dupont (échiquier infini), je vois à peu près comment faire pour trouver cette formule. Mais pour le tien, je suis un peu bloqué alors je remets à plus tard !
|
|
|
Ok, anselan Mais si le Roi s'arrête dès qu'il a atteint h8, on obtient un problème aussi intéressant, et peut-être plus "échiquéen". Y a-t-il une formule ? je n'en ai aucune idée !
|
|
|
a mathou L'idee que tu suggeres est dans la meme situation que la generalization propose par nicolas. Ils sont tous les deux plus difficile que le probleme de base. et a mon avis les solutions sont moins elegant.
|
|
|
pour une solution il faut diagonaliser une matrice 64x64
|
|
|
mouais mo12mo ... ... moi aussi j'ai pensé aux chaines de Markov (si c'est bien à ca que tu penses), mais il me semble que c'est un peu bourrin et pas dans l'esprit de ce qui est demandé. en plus il faudrait le nombre de chemin total, sinon on n'aurait acces qu'a la probabilité d'être en h8 à l'étape n et pas au nombre de chemins.
|
|
|
mouarf je suis déçu was problème de math c'est simple on note aij,n le nombre de façon d'aller de la case ij a h8 en n coups
de la case ij en un coup on va a ik
aij,n=somme(iktel |ik-ij|=1;aik,n-1)
ce qui nous An=(aik)=UAn-1
on diagonalise une matrice 64x64 et hop le tour est jouer
An=u^nA0
bon je suis pas rigoureux hein
France-Echecs: un nouvel article n'était pas vraiment nécessaire...
|
|
|
Effectivement je crois que ca marche (t'es pas tres clair mais avec un petit effort ca va) mais ceci dit pas bien sûr que ce soit l'idée mais c'estbien trouvé quand même.
|
|
|
a mo12om Bien fait pour avoir reconnu que c'est une question d'algebre lineare. Mais je cherche encore la formule exacte pour cette element de A^n. Avec ton approche, ce n'est pas simplement une question de "hop" :-) pour trouver cette formule. Je demande une maniere de voir la geometrie pour que la solution sort elegamment. Alors si c'est une question de math.
|
|
|
a anselan autrement dit tu attends une autre méthode ?
|
|
|
a dan31 ce n'est pas exactement une autre methode. la premiere etape est de reconnaitre qu'il faut diagonaliser bien la 64x64 matrice. mais ca c'est affreux comme tache, pas simplement une question de "hop"! Mais dans ce cas-ci, avec le roi sur l'echequier, les chiffres sont sympas. Comment voir que les chiffres sont si bien eleves? C'est ca la probleme.
|
|
|
heu...... quelqu'un peut traduire pour un non matheux?!
merci!
|
|
|
n pièces Combien y a-t-il de façons de choisir n pièces (pour une étude par exemple), En excluant les promotions?
Pour n=2 la réponse est 1 (facile).
Pour n=3 la réponse est 10.
Quelqu'un aurait-il une solution élégante pour n compris entre 4 et 32?
Peut-être une récurrence?
Ou alors la solution est elle connue?
|
|
|
Resultat
Un petit programme en Pascal montre (si on exclut les promotions) qu'
il y a 236 196 jeux de pièces possibles sur un échiquier.
Voici le nombre de jeu de pièces suivant le nombre total de pièces :
N = 2 ->1
N = 3 ->10
N = 4 ->53
N = 5 ->194
N = 6 ->546
N = 7 ->1254
N = 8 ->2445
N = 9 ->4170
N = 10 ->6378
N = 11 ->8940
N = 12 ->11697
N = 13 ->14484
N = 14 ->17109
N = 15 ->19320
N = 16 ->20820
N = 17 ->21354
N = 18 ->20820
N = 19 ->19320
N = 20 ->17109
N = 21 ->14484
N = 22 ->11697
N = 23 ->8940
N = 24 ->6378
N = 25 ->4170
N = 26 ->2445
N = 27 ->1254
N = 28 ->546
N = 29 ->194
N = 30 ->53
N = 31 ->10
N = 32 ->1
On remarque une symétrie (2+i et 32 - i ont le même nombre de solutions)
Même si ces dispositions de pièces ne sont pas toutes "équilibrées" (que penser de celle ou les Blancs ont toutes leurs pièces et les Noirs leur seul Roi par exemple), cela laisse de la marge aux compositeurs d'études !
|
|
|
La symétrie s'explique simplement Par le fait qu'outre les deux rois, il revient au même de choisir les pièces présente sur l'échiquier ou les pièces manquantes.
|
|
|
Oui Puch
Le problème peut se prendre par les deux bouts!
Pour les promotions ...
Si on veut une promotion blanche exactement :
Pour une promotion en Dame on obtient 104 976 jeux de pièces supplémentaires
Pour une promotion en Tour, Cavalier ou Fou on obtient 69 984 jeux de pièces supplémentaites dans chaque cas
Soit au total 209 952 + 104 976 = 314 928 jeux de pièces supplémentaires.
Si on accepte une promotion unique qu'elle soit blanche ou noire on obtient donc 629 856 + 236 196 (cas où il n'y a pas de promotion) = 866 052 jeux de pièces supplémentaires.
Donc on multiplie par 3.66 environ le nombre de jeux de pièces possibles en acceptant une promotion unique.
J'espère n'avoir pas commis d'erreurs !
Pour plus de promotions il y a un nombre assez élevé de cas à différencier
|
|
|
mon pc a lache durant la compilation du prog pour diagonaliser l'idée c'est de dire
on connait toutes aij,n qui correspondent aux nombre de façon de rejoindre la case h8 a partir de la case ij
en n+1 coups a partir de la case ij on fait d'abord 1 mouvement et on se retrouve a résoudre de le problème pécédent
aij,n+1=somme(ol tel que la case ol se trouve a un coup de ij , aij,n)
lamatrice est symetriqe positive doit se diagonalser
|
|
|
a mo12om Je suis d'accord avec ta logique, mais calculer les eigenvalues d'un telle grande matrice par PC me semble tres difficile et franchement ennuyeux.
L'interet dans cette probleme et devinir une maniere beaucoup plus elegante pour devinir ces 64 eigenvalues.
|
|
|
La dernière soutenance de projet est finie Je vais me mettre à chercher dans quel ordre écrire nos vecteurs de base pour rendre cette matrice sympathique...
|
|
|
Andrew, eigenvalue = valeur propre (en francais).
Sinon j'ai pas vraiment suivi la discussion. Quelle est la matrice 64x64 qu'il faut diagonaliser ?
|
|
|
nicolas merci pour la traduction. la matrice est la "matrice d'adjacence"??? ("adjacency matrix") de la graphe de 64 noeux, ou chaque noeux correspond a une case de l'echequier. Donc si les premiers rang/colonne correspond a a1,a2,a3,a4...a8;b1,b2,b3,b4... on va trouver que le premier rang/colonne de la matrice commence 0,1,0,0...0;1,1,0,0... etc.
|
|
|
Je repense à cet intéressant problème. Je ne sais pas si anselan est encore dans les parages. Une chose m'intrigue, je cite
"anselan, le 28/05/2004 - 13:22:34
on cherche une formule "closed", avec les operateurs +,-,*,/,^, et pour la rendre plus court, on admet aussi le fonction "round" pour trouver le nombre entier plus près"
S'agit-il vraiment de trouver une formule exacte pour tout n ou une formule approchée pour n grand sous la forme d'un équivalent en l'infini ?
Parce que j'ai du mal à comprendre qu'on puisse trouver une formule assez précise pour avoir une erreur inférieure à 0.5 (si on veut utiliser la fonction round ou arrondi), mais pas assez précise pour être complètement exacte.
|
|
|
J'imagine que Andrew a en tête des formules fermées mais pas explicites, comme des limites ou des intégrales.
|
|
|
parce qu'après réflexion j'ai trouvé un équivalent lorsque n tend vers l'infini (résolu seulement dans le cas d'un échiquier 4 x 4) que j'ai ensuite vérifié numériquement du type a x b ^ n ... avec valeurs explicites pour a et b mais je ne sais même pas si c'est ce genre de truc qu'il faut trouver.
|
|
|
en fait j'ai même une expression exacte dans le cas de l'échiquier 4 x 4 mais la démarche est pas terrible par rapport à celle qui me donne l'expression approchée, c'est du calcul assez bourrin.
|
|
|
Tiens! Apres toute cette periode d'absence, je me rappelle encore le mot de passe aleatoire & idiot de France-Echecs. Ca doit etre l'amour... :)
@Nicolas: non c'est une formule bien exacte! Et pour clarifier, le fonction "arondir" n'est que pour rendre un peu plus vite le calcul. Ce n'est pas necessaire.
On peu travailler avec une matrice 64x64 ("sparse" est le mot anglais) mais est-ce qu'on peut avour une idee pour le reduire beaucoup jusqua'a 8x8.
|
|
|
creuse
|
|
|
Je pense qu'au lieu de résoudre la matrice sur tout l'échiquier, nous pouvons nous contenter de résoudre sur le triangle A1-d4-d1.
|
|
|
f(n) = [-(-1)^n + sum (i=1…7 & j=1…7) d(i).d(j).[k(i)k(j)-1]^n] / 36
ou:
k(1) = 2,
k(2) = 1 + 2cos(1*pi/9),
k(3) = 1 + 2cos(2*pi/9),
k(4) = 1 + 2cos(4*pi/9),
k(5) = 1 + 2cos(5*pi/9),
k(6) = 1 + 2cos(7*pi/9),
k(7) = 1 + 2cos(8*pi/9),
et
d(1) = -1,
d(2) = -d(7) = 1/[(k(2)^2-k(2)+1)],
d(5) = -d(4) = 1/[(k(5)^2-k(5)+1)],
d(6) = -d(3) = 1/[(k(6)^2-k(6)+1)].
|
|
|
Ca peut s'ecrire aussi comme:
round[(sum (i=1…7 & j=1...7) I{|k(i)k(j)-1|>1}d(i)d(j)[k(i)k(j)-1]^n/)/36],
ou I{b} est une fonction logique: (1 si b est vrai, 0 si faux).
Pour n = 0,1,...,6, bien sur f(n) = 0, et puis
f(7)=1,
f(8)=56,
f(9)=1309,
f(10)=20370,
f(11)=255366,
f(12)=2782296,
Arondir nous donne une formule avec 19 termes, le dominant etant d(2)^2 . [k(1)^2-1]^n, a peu pres 0.000676 * 7.29^n.
Alors pourquoi? Je vais expliquer quand je reviens ce soir.
|
|
|
Il y a deux idees pour resoudre ce probleme. Le premier se montre dans la composition suivante:
(6+4) Combien de mats de series dans exactement n coups?
A.Buchanan: 1er Prix :)
Tournoi de la 80eme Anniversaire d'Eero Bonsdorff
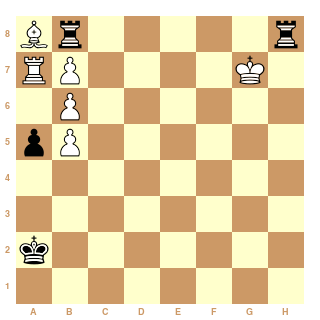
Normalement le roi entre dans une case adjacente:
1 1 1
1 0 1
1 1 1
Mais s'il dort, alors il y a une neuvieme possibilite:
1 1 1
1 1 1
1 1 1
Quand la tour blanche se bouge, ca permet que le roi dort pour ce tour. La raison pourquoi c'est interessante est que maintenant on peut separer le composant horizontale du composant verticale dans le mouvement du roi.
Dans l'axe X, il y a 6x1 cases. C'est "assez facile" a calculer X(n) = la quantite de chemins pour que le roi commence a la case 5 sur 6, et arrive a la case 1 apres exactement n coups.
Dans l'axe Y, il y a 1x7 cases. Dans la meme maniere on peut calculer Y(n) = la quantite de chemins pour que le roi commence a la case 7 sur 7 et arrive a la case 2 apres exactement n coup.
La solution de notre probleme est simplement f_X(n)*f_Y(n).
Mettons m=n-1, puis pour toute n>=0:
f_X(n) = rond[ ( (_/3+1)^m - 3.2^m) / 12 ]
f_Y(n) = rond[ ( v_/(2-v)[_/(2+v)+1]^m – 2v[v+1]^m + v_/(2+v)[_/(2-v)+1]^m) / 16 ]
ou: _/ indique la racine carree positive
et: v = _/2.
Alors la quantite de solutions s'agrandit comme, O([(_/3+1)(_/(2+v)+1)]^m), a peu pres 7.78^m.
La deuxieme idee est qu'on n'a pas besoin de la tour pour jouer ce jeu du roi qui dort! (A la prochaine reponse...:))
|
|
|
Un peu de theorie de matrices, helas...
Supposons que M = la matrice de adjacence pour le roi sur l'echequier. C'est a dire que M est 64x64, et chaque rang correspond a une case sur l'echequier et chaque colonne egalement colonne. M_i,j = 1 si un roi peut balader de la case i jusqu'a la case j dans un coup. Sinon, M_i,j = 0.
Les matrices fonctionnent un peu comme les chiffres, et on peut bien multiplier deux matrices carrees ensemble pour creer une troisieme. Dans le jeu d'echecs, la quantite de chemins different pour aller de case i a case j dans exactement n coups est donne par (M^n)_i,j ou M^n indique multiplication de matrice M par soi-meme n fois.
Notons que M^0 est la matrice I qui est zero sauf sur la diagonale majeur I_i,i. I est nomme l'identite et joue un role archi-important dans la theorie de matrices, un peu comme le chiffre 1 pour les numeros.
Maintenant de la magie: je vous encourage a me croire que pour chaque matrice symmetrique, il existe une matrice D et son "inverse" D' pour que A = D.M.D' est diagonale, et D.D' = D'.D = I. C'est a dire que A_i,j = 0 sauf quand i = j.
Pour chaque paire de cases, on peut donc calculer la quantite de chemins dans n coups comme:
somme (i=1...64) c_i * e_i^n
ou e_i sont les chiffres sur la diagonale majeur de D.M'D.
et c_i sont des constants qui dependent les deux cases selectionnees.
Alors considerons le roi-qui-dort-de-temps-en-temps. Il peut passer un coup restant sur la case ou il se trouve actuellement. Donc la matrice d'adjacence, N, pour lui = M+I.. Mais la quantite de chemins est:
somme (i=1...64) c_i * (e_i+1)^n
Donc pour resoudre la probleme, on peut calculer (assez facilement) les chemins pour le roi qui dort, en considerant les deux axes separamment. Dans une axe, ca donne:
somme (i=1...8) d_i * f_i^n
La quantite de chemins dans deux dimenions est:
somme (j=1...8)(k=1...8) d_j * d_k * (f_j * f_k)^n
Et puis pour le roi ordinaire:
somme (j=1...8)(k=1...8) d_j * d_k * (f_j * f_k - 1)^n
Et voila!
|
|
|
La réponse au pb d'origine serait-elle là :
http://oeis.org/A025597
à+
É.
|
|
|
Merci beaucoup, Éric,
Je vais essayer d'ajouter la formule à OEIS.(Aussi-tot qu'on me donne une compte).
|
|
|
Monsieur Gibson qui a cree l'article en OEIS m'a repondu. Il n'a aucune formule: simplement il a cree des donnees avec son ordinateur.
La formule la plus economique que j'ai est:
f(n) = (4/81) * sum(j=1...8, k=1...8) [(-1)^(j+k)] * [sin(j*pi/9)*sin(k*pi/9)]^2 * [(1+2cos(j*pi/9)*(1+2cos(k*pi/9)-1]^n
Les elements trigonometrique peuvent etre ecrits avec racines cubiques. Les racines quadratiques ne suffisent pas car 9 n'est pas un produit de nombres premiers de Fermat.
Maintenant je vais essayer d'ecrire une tres petite article pour "Mathematical Magazine" aux Etats Unis.
|
|
|
une réponse 8 ans après !!?
|
|
|
@ Andrew,
Il y a une jolie photo de toi dans "chess composition", que Eric Huber a publié à l'occasion de ton anniversaire. C'est quoi le costume, celui des anciens d'une grande école ?
|
|
|
@Esoxlucius:
Eh bien... j'etais occupe! Mais effectivement Pessoa etait sur la bonne piste tres tot. Helas il ne l'a pas suivit.
@Nicolas:
Pour celebrer l'anniversaire d'un copain de la "grande ecole", je me suis mis en costume de cardinale catholique. On etait tous en costumes variees. Mais j'ai passe aussi un vendredi apres-midi amusant au bureau dans la meme costume...
|
|
|
"La formule la plus economique que j'ai est:
"f(n) = (4/81) * sum(j=1...8, k=1...8) [(-1)^(j+k)] * [sin(j*pi/9)*sin(k*pi/9)]^2 * [(1+2cos(j*pi/9)*(1+2cos(k*pi/9)-1]^n"
Mais helas un peu *trop* economique avec les parentheses - j'avais paume deux. Sinon, c'est bon je crois. (Merci, Mario)
f(n) = (4/81) * sum(j=1...8, k=1...8) [(-1)^(j+k)] * [sin(j*pi/9)*sin(k*pi/9)]^2 * [(1+2cos(j*pi/9))*(1+2cos(k*pi/9))-1]^n
|
|
|
Existe-t-il, à votre conaissance, un livre compilant toutes les recherches mathématiques sur le jeu d'échecs ?
Les travaux de Gauss, Euler .....
|
|
|
Il y avait bien un bouquin de Kraitchik, mais les solutions à divers problèmes ont probablement bien évolué depuis
|
|
|
@Blaise: je crois qu'il n'y a pas de tel livre encyclopédique. Il y a "Mathematics and Chess" par Miodrag Petkovic, publié par Dover, mais c'est un peu sec, peut-être. Noam Elkies a enseigné un cour a Harvard sur le sujet pendant quelques années, et depuis dix ans est en train d'écrire un livre sur ce sujet avec Richard Stanley de MIT. Il y a des autres enthousiastes qui ont des sites d'Internet interessantes comme Mario Velucchi et George Jelliss. Sur wikipedia la meilleur page pour l'instant est: http://en.wikipedia.org/wiki/Category:Mathematical_chess_problems.
Si vous voulez discuter plus sur ce sujet par email, dites-moi.
|
|
|



