|
| Cavaliers d'avril par ins7281 le
[Aller à la fin] |
| Problèmes | |
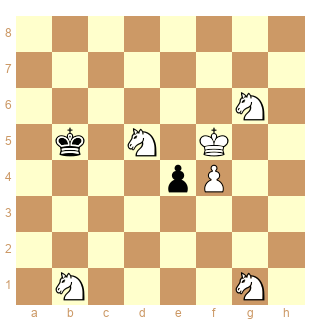
Oroy. Inédit pour France-Echecs.
Mat aidé en 3 coups.
Vous avez 4 jours pour trouver.
|
|
|
Plus que 3 jours.
|
|
|
Bien sûr le problème ne respecte pas les conventions habituelles, mais le 1er avril, tout est permis !
|
|
|
Je vois qu'on s'est compris.
|
|
|
Faut separer, Oroy 3 jours pour le commun des mortels, mais seulement 3 minutes pour Francois...
|
|
|
Il n'a pas dit qu'il a trouvé la solution. Car il n'y a pas besoin de la connaître pour voir que je n'ai pas respecté les conventions. ;-)
|
|
|
Il est magnifique ! Miroir...mon beau miroir est-ce que je suis un modèle parfait ??
|
|
|
Oui ! c'est une nouvelle variété de masque de carnaval : moins de couleurs, plus de lumière,
|
|
|
J'ai un doute affreux Je ne trouve pas, mais...
1e avril + remarque de FPC + position particulière de deux éléments me font envisager une possibilité qui ne respecte pas grand chose (mais Oroy est un rebelle !) mais qui marche !
|
|
|
Ouaip Bravo Oroy ! Clé irrévérencieuse bien sûr, mais tableau de mat étincelant. ;o)
|
|
|
4x2+1=9
|
|
|
Josef Moravec proposait d'admettre la prise en passant sans démonstration lorsqu'il n'y avait pas d'autre solution. Je regrette aujourd'hui de ne pas avoir soutenu cette idée qui est la plus féconde. Mais je me suis laissé 'bourré le mou' par Lapierre avec le fameux argument : on accepte le roque car le plus probable est qu'il soit valide, on refuse la prise en passant car le plus probable est qu'elle soit invalide. Or, c'est un argument douteux : si on compare ces deux probabilités, surtout dans les positions de problèmes avec AR, on est loin du compte. In memoriam Josef Moravec.
|
|
|
Erratum 'bourrer le mou'
|
|
|
Un opinion Voir ma contribution sur la convention a posteriori dans un autre fil...
- Je suis pour l'argument Dura Lex, sed Lex, donc pour moi ce problème est incorrect et c'est tout, dès lors que les lois sont edictées...
- L'argument de Lapierre me ^paraît douteux aussi. Pour les conventions, je pense qu'"on accepte le roque si l'AR ne l'interdit pas", parce qu'il est impossible de démontrer la légalité du roque dans une position donnée, alors qu'il est possible, le cas échéant, de démontrer son impossibilité. Ce n'est pas un question de "probabilité" (d'ailleurs, j'ai du mal à voir comment on définrait la "probabilité" de la légalité du roque)
- Ca ne marche pas pour la prise en passant, selon le cas, on peut démontrer sa possibilité, son impossibilité ou ne pas pouvoir conclure... Sans doute, ce qui a emporté la décision du "législateur" est la fécondité de la convention, et l'historique (les premiers problèmes d'AR étaient sûrement du genre 'montrer que la pep est possible, puis mater', plutôt que 'montrer que la pep est impossible' - moindre effet de surprise)
|
|
|
UnE opinion ! Je confonds le genres, sûrement mon côté féministe ! ;-)
|
|
|
Ceci dit Le mat est joli, mais le serait tout autant sans le "poisson d'avril" qui va avec...
|
|
|
Je te comprends, pessoa. Je pourrais très facilement rendre le problème conforme à Dura Lex, sed Lex en plaçant le Pf4 en f3, car cela n'introduit aucune démolition. (En aparté, j'aspire fortement à une autre conception de la Justice : je la souhaite juste plutôt que dure.)
L'argument de Lapierre n'a pas été inventé par lui, je ne sais qui l'a proposé, mais il a été presque unanimement adopté pour fixer les premières conventions de l'AR.
La probabilité de la prise en passant légale est facile à calculer : c'est 1 divisé par le nombre de coups possibles pour le camp qui était au trait lors du demi-coup précédent.
Pour la probabilité de la légalité du roque, si on ne peut la calculer, on peut au moins en donner une approximation: prob~= 1-((tmc-mcc)/tmc) puissance(lgp) avec
lgp:longueur de la PCPJ menant à la position.
tmc:nombre moyen de coups à la disposition du camp dont on évalue la probabilité du roque.
mcc:nombre moyen de ce total moyen de coups qui cassent le roque.
Exemple: Il faut 20 coups pour atteindre la position. Il y a 30 coups jouables en moyenne, dont 3 qui cassent le roque.
prob= 1-((30-3)/30)) puissance 20 = 0,12.
Dès le 3ème ou 4ème coup le nombre de 3 coups en moyenne cassant le roque est très sous-évalué, je l'ai fait exprès pour éviter qu'on m'objecte que j'avais sur-estimé cette valeur pour servir mon argumentation.
Quant à la probabilité de la pep, calculée comme je le propose, elle est beaucoup plus forte dans le genre de problèmes qui nous intéresse que dans les positions quelconque prises dans le domaine de la partie pratique. C'est pourquoi 'l'argument dit de Lapierre' à l'origine de toutes les conventions de l'AR me paraît d'une valeur douteuse.
Quant à la convention de Moravec elle serait plus féconde sans nuire à l'AR classique, exigeant des justifications, car cette convention ne s'applique que lorsqu'il n'y a pas d'autre solution. Je voudrais avoir l'avis de Michel Caillaud sur cette question. Mais il me semble qu'à l'époque où ces débats ont eu lieu, l'influence de Luigi Ceriani, magister de l'AR, était prépondérante.
Ouf ! j'espère ne m'être pas planté.
|
|
|
Suite pour pessoa: Même rebelle, j'ai quand même attendu le 1er avril pour publier ce problème, qui n'est pas non plus conforme à la règle qui veut qu'on n'utilise pas de pièces promues dans la position de départ. N'y aurait-il pas avantage à assouplir cette exigence pour un certain nombre de problèmes ? Ici de l'AR, là des promotions dans le jeu, où, comme dans le cas présent, un task (mat parfait).
|
|
|
Pessoa... Je ne suis pas d'accord pour reconnaître qu"'il est impossible de démontrer la légalité du roque dans une position donnée".
Pas le temps ce soir, mais je te retrouverai demain le lien vers une ou deux positions 9.6 où la légalité du roque est démontrable.
|
|
|
|
Les anciens de FE savent bien que l'on peut prouver que le roque est possible. 
DR. Trait aux blancs. Dernier coup ?
Je cherche le premier exemple 'historique' sur FE.
|
|
|
|
Correction que l'on peut prouver que le roque est possible. 
DR. Trait aux blancs. Dernier coup ?
Je cherche le premier exemple 'historique' sur FE.
|
|
|
Ref Proba Ouhla voilà une approche qui me semble un poil simpliste Oroy ! Tu postulesen fait simplement que l'ensemble des coups sont parfaitement équiprobables.
Comme 2ème coup, dire que p(2. Re2) = p(2. Cf3) me semble largementcontestable !Je pense que pessoa s'appuyait sur une logique bcp + simple. A savoirsur l'ensemble des positions fréquemment jouées, il est massivement plusfréquent d'avoir droit au roque que d'avoir droit à la pep.
|
|
|
|
Ha non oups (réveil dur) en fait ça n'est pas la position de pessoa qui juge prudemment que la probaappliquée ici est un procédé à la valeur douteuse. Il est vrai que mon message ci-dessus ne vaut que si l'on tente de faire le pontavec le jeu réel. En pur monde de composition c'est moins vrai encore que làaussi il y ait à mon sens peu de chances pour que l'ensemble des coups soientéquiprobables.
Un autre raisonnement pourrait tabler sur le fait que la pep est "moins probable"du fait qu'elle a la même proba que "un pion blanc/noir vient d'avancerde 2 cases tandis qu'un pion noir/blanc était situé sur la 4/5ème rangéesur une colonne voisine de celle du premier". Bon alors regicide cette position ? :o)Il me semble en effet que ça me dit quelque chose ce truc. Pour que çasoit tout à fait convaincant il faut une position seule, càd sans infosupplémentaire du style "n coups ont été joués jusqu'ici", ou "mat en x" (oeufcorse :o) ). Le trait est tolérable, mais il faudrait aussi que le roque soit nonseulement légal mais aussi possible, sans quoi moi je te sors la positioninitiale et le tour est joué :o).
|
|
|
Au sujet de la "probabilité", c'est Perestroïka qui a compris ce que voulais dire. merci Peres !
Je pense qu'il n'y a pas un moyen "évident" de "probabiliser" le passé d'une position d'échecs. Sans vouloir entrer dans une discussion philosophique sur le hasard (pitié !!), pour utiliser cette merveille qu'est la calcul de probabilité, on est obligé de faire des hypothèses du type "toutes les faces d'un dé ont la même probabilité de sortir", c'est-à-dire de supposer que telle ou telle partie du phénomène que l'on observe est soumise au hasard. Pour la lancer d'un dé "non truqué", l'hypothèse que je viens de donner est admissible par le sens commun, je ne vois pas d'hypothèse admissible par le sens commun pour une position d'échecs dont on sait qu'elle a été forgé par l'esprit tordu d'un compositeur. Comme Oroy, je trouve donc douteux l'argument dit de Lapierre...Pour FPC, c'est vrai que quand je dis qu'on ne peut pas prouver que le roque est légal, je néglige la cas de la règle 9.6 (voilà longtemps qu'on n'en avait pas parlé, de celle-là ! Au fait, est-ce vraiment une convention "officielle" ?). J'espérais (naïvement, certes...) que ça ne se verrait pas, pourtant je venais justement de lire le fil dont tu parles ! C'est celui-ci : Présomption de légalité Et d'une manière générale, tous les posts de cette époque sont passionnants ! Au fait, Anselan ne vient plus trop sur France-echecs et c'est bien dommage !
|
|
|
Ha oui c'est ce lien pessoa ! Ca remplit toutes les conditions en effet.
|
|
|
Oups pas de titre J'aurais pu mettre "hasard", ça attire toujours le public.
Puis je vois que c'est regicide qui parle le premier du cas particulier "9.6", pardon !Pour Oroy : bien sûr qu'on peut faire des entorses. Les cavaliers de promotion sont admissibles puisque tu présentes un mat parfait avec 4 cavaliers (encore que, ç'aurait été plus spectaculaire avec des canassons promus en cours de solution). Et l'entorse aux conventions sur l'AR est justifiée par la date !
|
|
|
Nostalgie Merci pour ce lien, pessoa. Ah ! c'était le bon temps...
|
|
|
pessoa, si tu trouves douteux l'argument dit 'de Lapierre', approuve-tu pour autant mon calcul de probabilité ? Je n'ai pas l'impression, au vu de la façon dont tu envisages la chose.
Pour ma part, je m'en suis tenu strictement aux principes énoncés par Pascal (oui, Blaise): je dénombre (approximativement, car je ne peux pas faire autrement) tous les cas, puis tous ceux qui ne cassent pas le roque, etc. Il y a assez de prof. de maths sur ce site pour expliquer la méthode, qui malgré son imprécision suffit me semble-t-il à montrer que l'argument 'Lapierre' est douteux.
Mais ceci ne veut nullement dire qu'il faille abroger les conventions existantes, sur lesquelles reposent des milliers de petites merveilles.
|
|
|
erratum: approuves-tu
|
|
|
Pas besoin de prof de math pour voir où est ton erreur ! Je m'auto-cites : Tu postules en fait simplement que l'ensemble descoups sont parfaitement équiprobables.
Voilà l'hypothèse que tu fais implicitement et qui est probablement très discutable !
|
|
|
"m'auto-cite" oups !
|
|
|
Pas en composition Puisqu'on ne s'attache pas à savoir si un coup est bon ou pas. Il n'y a que des possibilités, pas de gaffe ou de sacrifice stratégique ( et on ne cherchera pas à estimer le niveau Elo des protagonistes ! :-D ).
|
|
|
Cela dit, pessoa, je m'aperçois que j'ai fait une erreur dans mon calcul car j'ai oublié de le terminer par la soustraction. Dans mon exemple, 12% est le probabilité que le roque ne soit pas cassé, donc 88% qu'il soit cassé. C'est énorme malgré la faiblesse du nombre moyen de coups (3) cassant le roque à chaque niveau d'avancement de la partie. Pour faire jeu égal, la prise en passant requiert dans ce cas 7 coups possibles autres que l'avance du Pion de 2 pas.
|
|
|
Ref atms Même en composition certaines positions sont plus fréquentes que d'autres, ne crois-tupas ?
En tout état de cause je ne vois pas comment on pourrait démontrer ou ne serait-ceque défendre une certaine équiprobabilité... Non j'vois pô !
|
|
|
Pour Oroy (attention, c'est long !) Je me répète : pour appliquer le calcul des probabilités à un phénomène, il faut considérer qu'il est aléatoire. Or, à mon sens, une composition, avec ou sans AR, n'est pas aléatoire. Mais à la limite, pourquoi pas...
D'autre part, dans ton calcul, tu fais les hypothèses suivantes : tous les coups sont équiprobables, et la position est issue d'une pcpj. Or, ces hypothèses sont, elles aussi, des conventions ! Et comme ces conventions ne font l'objet d'aucun consensus (la preuve, Peres et atms ne sont pas d'accord sur la question), elles sont (pour l'instant) peu justifiables...
Enfin, je ne suis pas non plus d'accord avec ton calcul sur la probabilité du roque, pas du tout !!
Tu considères une position issue d'une pcpj de 20 coups (pas nécessairement unique). Or, la formule que tu donnes (à supposer que 30 possibilités dont 3 qui cassent le roque soient des hypothèses correctes, déjà je doute, à mon avis c'est plus dès que le roi et/ou la tour ont du champ, et ça passe à 0 dès que le roque est déjà cassé !), la formule que tu donnes, donc, correspond à la probabilité qu'un partie QUELCONQUE de 20 coups ait le roque "cassé". Or, on sait à l'évidence que la partie n'a pas été quelconque, puisqu'on a la position au 20ème coup !
Une "probabilisation" plus adéquate serait, par exemple, de considérer TOUTES les pcpj menant à la position donnée. Si on suppose qu'elles sont toutes équiprobables, la probabilité que le roque soit cassé est de Nc/N avec
N nombre de pcpj différentes menant à la position du diagramme
Nc : parmi ces pcpj, nombre de parties où le roque est cassé.
A mon avis, cette probabilisation conduit à une probabilité de roque forte dans la plupart des cas, voire parfois de 100%. En effet, si dans la position du diagramme le roi blanc est en e1 et une tour blanche en h1 (par exemple), je ne pense qu'on puisse trouver systématiquement un pcpj qui comprenne un "aller-retour" du roi ou de la tour, ou l'arrivée en h1 de l'autre tour, ou encore d'une tour issue de promotion (c'est-à-dire d'avoir un roque cassé). C'est sans doute possible si, au diagramme, il y a plus de "coups apparents" noirs que blancs, par exemple, mais ça ne saurait être vrai en général.Pour résumer ce que je conteste dans tes propos :
- Je ne partage pas a priori les hypothèses que tu donnes pour "probabiliser" le passé d'une position d'échecs : dire qu'elle est issue d'une pcpj, dire que tous les coups passés sont équiprobables, et même de considérer que les probabilités s'appliquent ! Bref, dire qu'on est dans le cadre de Blaise Pascal.
- Je pense que le calcul que tu donnes est erroné.
- Je pense, mais c'est accessoire, que l'hypothèse "en moyenne 3 coups sur 30 cassent le roque" est douteuse...
- Je pense que dans le cadre probabiliste que tu proposes, un roque apparent est, le plus souvent, probable, voire certain ! Au plaisir de débattre !
|
|
|
ceci dit Je suis d'accord sur un point : cette histoire de probas ne devrait pas remettre en cause les conventions actuelles sur le roque la pep, qui sont les plus fécondes, sans doute.
|
|
|



