|
| A quoi sert l'opposition ? par kaktus le
[Aller à la fin] |
| Finales | |
Ceci n'est pas une question à caractère politique!!
Dans certains livres sur les finales de pions, on présente d'abord le concept d'opposition, puis l'opposition diagonale, puis l'opposition éloignée, jusque là, tout va bien, on trouve des cas de figures où ces outils s'appliquent.
Mais ensuite, il arrive qu'on enchaine sur "l'opposition diagonale éloignée", voire, "l'ultra opposition" :
quand les 2 rois sont séparés par un rectangle aux côtés impairs (ou en clair, un rectangle aux 4 coins de la même couleur).
Démonstration à l'appui, on nous montre que 2 rois nus sont virtuellement en opposition.
Certes, mais en dehors de la satisfaction géométrique, quelqu'un aurait-il sous la main un exemple concret où ces particularités géométriques ont une utilité pour résoudre une position ?
|
|
|
Pour faire simpliste et rapide Toutes ces oppositions que tu décris permettent à celui qui la détient théoriquement de forcer la venue de l'opposition "classique" s'il le souhaite.
|
|
|
oui Sisyphus, ça j'ai bien compris mais peux tu me trouver un exemple concret ou une étude où l'on s'en sert ?
(Je parle des 2 derniers types)
|
|
|
par ex ( Chéron y consacre 9 pages) Frantisek Dedrle, 1921 : trait aux Noirs, gain blanc ; trait aux Blancs : nulle

|
|
|
ah ok. je vois bien l'utilité de l'opposition avec le trait aux blancs.
Par contre, avec le trait aux noirs, je trouve que c'est moins clair :
1...a5 2.Rg7 (ultra opposition)
2...Ra4 et là, je ne vois pas pourquoi 3.Rf6 ne marche pas.. ?
Si les noirs prennent l'ultra opposition avec :
3....Rb4 4.Re6.
4...Rc4 (opposition diagonale) 5.Re6 et les blancs ont l'air de gagner.
En tout cas merci pour l'exemple.
Est-ce que tu en as un aussi avec l'opposition diagonale éloignée ?
|
|
|
oui, 5.Rd6 +- trait aux Noirs, GAIN blanc. Pour l'instant, ce sera tout.
|
|
|
Tu veux peut-être quelque chose comme : J.Moravec, Prace 1951, 1ère mention d'honneur
 Nulle. Nulle.
|
|
|
erreur, la position est : Rh4,pd3,d4,e7/Re8,pd5,d6,f6. Nulle toujours.
|
|
|

J'ai besoin de voir :)
|
|
|

J'ai besoin de voir :)
|
|
|
la solution ? 1.Rg4! (1.Rh5? Rxe7) 1...Rxe7 2.Rh5! (2.Rf5? Rf7 ; 2.Rf4? Rf8! 3.Rg4 Rg7 4.Rh5 Rh7!) 2...Rf7 3.Rh6! Re7 4.Rh5 Re6 5.Rg6 Re7 6.Rh5 =
|
|
|
jvoulais dire le position :) pour justifier mes schémas précédents :)
Pour la solution, c'est plus dur pour moi, il va falloir que je prenne un peu de temps pour bien tout comprendre :)
|
|
|
ces situations sont très rares sur l'échiquier moi jconnais juste les principes de l'opposition et après je réfléchis quand il le faut.
C'est surtout important pour les problémistes
|
|
|
Dans un ouvrage
en voie de disparition, on lit ceci (p. 105), à propos d'un exemple similaire à celui d'Etyoud :
"L' opposition "rectangulaire" ou "diagonale" n'a de sens que par rapport aux accidents de l'échiquier [...] Une application simpliste de ces concepts conduirait en effet les deux Rois à se contempler indéfiniment comme des chiens de faïence" [...] Il faut savoir perdre l'opposition... pour la regagner". Et, après un contre-exemple, "ainsi les Echecs se vengent-ils avec humour de toutes les tentatives de mathématisation outrancières".
Cette dernière phrase aurait pu être dédiée à un bizarre promeneur québécois... qui nous a quittés.
|
|
|
Passage de l'opposition rectangulaire à l'opposition simple
Dans la variante de Kaktus, le RN est perdu en a4. A Rf6 il faudrait répondre ...Rb6!, ce qu'il aurait fait s'il s'était trouvé en a5.
Ce qui explique la nulle, trait aux Blancs : 1 Rg7 Ra5! (Ra7! aussi) 2 Rf6 Rb6!. Admettons tout de même que la règle du rectangle dont les côtés ont une longueur impaire fait gagner du temps dans les calculs.
|
|
|
Plus exactement "du rectangle dont chaque côté fait un nombre impair de cases".
|
|
|
Un concept découvert dans votre ouvrage AV, Caesar
|
|
|
Ouah ! Impérial Ave, fils d'Atlas.
|
|
|
ref dulovitch, j'ai tendance à penser comme toi, mais ça m'envoie des des labyrinthes complexes. C'est pour ça que je suis à l'affût de ce genre de techniques qui pourraient éventuellement soulager des calculs.
Je suis également perplexes su les exemples donnés pour justifier l'existence de ces principes, ile me semblent rares et souvent soumis à l'exeption signalée par Erony dont j'ai vérifié l'authenticité dans le livre rare ;)
Quant au deuxième exemple d'eytoud, j'ai eu beaucoup de mal à le résoudre, surtout à le raccrocher à un petit outil comme "opposition rectangulaire au autre", même si je sens qu'il a des cases conjuguées(e7 et h5, je me mouille pas:), je n'ai pas encore fait le tour de la question avec le pion volage en f6.
En bref, après l'opposition basique, quelques zugzamb de bases (triangulation) ne doit on pas plutôt se raccrocher à une multiplicité d'exemples plutôt que d'en chercher une'essence commune ??
|
|
|
zugzamb-ie ou èze ? Quelques notes complémentaires alors pour l'étude de Moravec : essai 1.Rh5? Rxe7 2.Rg4 (2.Rg6 Re6 zz -+) 2...Rf8 ! (2...Rf7? 3.Rf5 zz =)3.Rf4 Rg7 (3.Rf5? Rf7 zz -+) 4.Rg4 Rg6 -+ Solution : après 1.Rg4! Rxe7 2.Rh5!! (puisque 2.Rf5? Rf7! à nouveau ou 2.Rf4? Rf8! 3.Rf4 Rg7 4.Rh5 Rh7! -+) 2...Rf7 3.Rh6! Re7(3...f5 4.Rg5 Re6 5.Rh4! Rf6 6.Rh5! et là on retrouve une autre étude didactique de Moravec : Rg4,pf4,h5/Re4,ph6 - 1.Rg3! Rd5! 2.Rh3(h4)! Rd4 3.Rh4(3) Rd5 4.Rg3 Rd6 5.Rf3 +- il y a des pertes de temps possibles) 4.Rh5! (4.Rg6? Re6 zz -+)4...Re6 5.Rg6 (zz) Re7 6.Rh5 nullité positionnelle.
|
|
|
je rajoute l'annexe de Moravec au cœur de la prenthèse :

|
|
|
A un ami cultivé
mais qui n'ose pas intervenir :
C'est exact, j'ai confondu le fils et le gendre. Mais avouez qu'Atlas a tout de même plus de gueule. Et le spécialiste en rochers, c'est bien lui.
|
|
|
Aucune provoc dans ce titre, je ne subodore nullement que les habituels lecteurs de FE soient "nuls", je me contente de parier que la surprenante clé de l'étude suivante peut être comprise par un quasi débutant. En allant pas à pas, s'il le faut.
Mais auparavant je vous laisse un peu réfléchir. Ceux qui, dans l'article voisin sur Lasker/Reichhelm, ont prouvé, ou annoncé, leur maîtrise de ce thème ont une excellente occasion de briller : ils ont dix minutes !
Pour les autres, un tuyau : l'application aveugle d'une certaine règle mène à une déconvenue. Cherchez les cases-clés, les emplacements où le Roi blanc aimerait bien se trouver, en laissant le trait, bien sûr, à son adversaire.
Les Blancs gagnent (K. Ebersz, 1935).
A bientôt.

|
|
|
Je crois que j'ai le réseau. Je propose (attention, solution, peut-être fausse d'ailleurs) 1 Rd2 ! et non 1 Re2 ? Rd8 !
Après, il y a subtilités sur les coups de pion, sans doute.
|
|
|
Exact, pessoa
Coups de pions : non, ...f6 n'étant jamais envisageable. Quand j'opposais cette étude aux "pions bloqués" de Lasker/Reichhelm, c'était pour signaler une position "ouverte" et donc plus naturelle. Et la notion de "plus court chemin" exposée par Kloch n'existe pas ici, car il n'y a qu'un foyer, d'où se construit tout le réseau.
|
|
|
J'ai du mal si j'ai bien vu que Re2 perd l'opposition sur Rd8, je n'ai pas encore trouvé la position de zuqzwang réciproque à atteindre, Rf6/Rf8 semble en être une, mais impossible de forcer cette position il me semble... Un petit indice ?
|
|
|
f6/f8
est bien le "foyer". Cherchez alors la conjuguée de e5, puis de d5. Vous en déduirez celle de f5, puis e4, f4 et tout s'enchaînera.
|
|
|
Solution et explications demain.
|
|
|
Position bien sympa en effet
|
|
|
N'aimeriez-vous pas avoir les Blancs ici, en laissant le trait aux Noirs ?
Trait aux Noirs : ils sont écrasés. Trait aux Blancs : on ne passe pas.
Les cases f6 et f8 sont conjuguées. Facile, n'est-ce pas ?

|
|
|
Même réponse.
Les cases e5 et e7 sont conjuguées.

|
|
|
Même réponse.
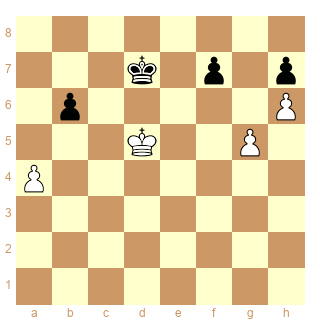
Les cases d5 et d7 sont conjuguées. Vous me suivez toujours ?
|
|
|
Trait aux Noirs, elle n'est guère reluisante : si le Roi noir vient en f8, alors le Roi blanc joue en f6, et c'est perdu, comme nous l'avons vu. Mais si le Roi noir vient en e7, alors son homologue joue en e5, et ce n'est guère mieux, nous l'avons vu également.
Mais si le trait est aux Blancs, les Noirs respirent : sur Rf6, ils répondent Rf8! et sur Re5, ils jouent avec sang-froid Re7!
Nous venons sans effort d'établir un premier résultat non trivial : Les cases f5 et e8 sont conjuguées.

|
|
|
Il vise trois cases : d5, e5 et f5. En vertu de ce qui précède, le Roi noir aimerait bien :
-- à Rd5 répliquer ...Rd7!
-- à Re5 répliquer ...Re7!
-- à Rf5 répliquer ...Re8!
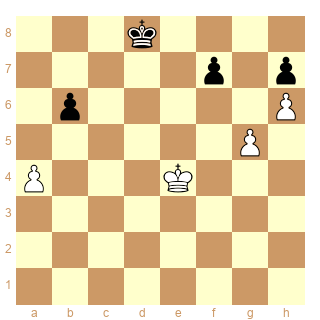
Comment est-ce possible ? Mais s'il est en d8, bien sûr. Les cases e4 et d8 sont conjuguées. Ce n'est pas trivial non plus.
Trait aux Blancs : nulle. Trait aux Noirs : ils perdent.
|
|
|
Imaginons le RN en e6. Soyez bien attentifs.
Donnons le trait aux Noirs :
-- ...Rd7 est contré par Rd5 comme déjà vu
-- ...Re7 est contré par Re5 comme déjà vu
-- ...Rd6 est contré par Rf5 visant f6 puis le Ph7 et de nouveau ...Re7 est contré par Re5
-- ...f6 n'apporte aucun soulagement : gxf6, ...Rxf6, Rd5 et le pion "a" gagnera la course.
Mais trait aux Blancs, tout danger est écarté :
-- Rd4 est contré par ...Rf5 et cette fois le Pf7 arrivera le premier
-- Rf4 est venimeux, s'apprêtant à conquérir la case f5. Mais réfléchissons : quelle est la case conjuguée de f5 ? Ne répondez pas tous en même temps. Oui, bravo, c'est e8 ! Vous suivez mieux qu'un élève moyen de classe de sixième. Pour être en mesure de répondre ...Re8, il faut donc jouer ...Rd7!! avec dans chaque cas une réplique toute prête : sur Rf5, ....Re8! , sur Re5, ...Re7! et, vous ne l'avez pas oublié, sur Re4, ...Rd8!.
Nous venons d'établir à la fois que les cases e4 et e6 sont conjuguées et que les cases f4 et d7 sont conjuguées.
Oui, e4 est en correspondance à la fois avec d8 et avec e6. Cela arrive souvent, il ne faut pas s'inquiéter.
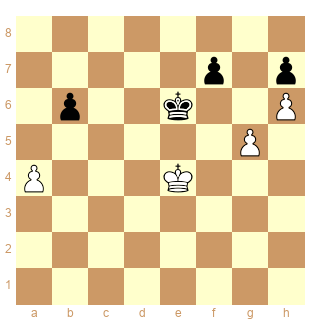
Quelques secondes supplémentaires de réflexion nous montrent que d4 et d6 sont aussi conjuguées. Il n'y a pas de problème en revanche côté ouest : sur un Rc4 blanc, le Roi noir n'est nullement tenu de s'opposer en c6. Il lui suffit d’attendre Rb5, après quoi il peut :
-- soit s'opposer en b7
-- soit se contenter de ...Rc7, puisque Ra6, ...Rc6 est sans danger
|
|
|
Petite pause de cinq minutes allez boire un verre.
|
|
|
Boire plutôt le contenu du verre.
|
|
|
Trait aux Blancs : nulle. Trait aux Noirs : ils perdent.
Vous avez bien en tête le réseau de cases conjuguées. Résumé des épisodes précédents : f6/f8, e5/e7, d5/d7, f5/e8, e4/d8, f4/d7, e4/e6 et d4/d6.
Les Blancs au trait peuvent placer le Roi sur d4, e4 ou f4. Les conjuguées respectives de ces trois cases sont d6, d8 et d7. Il est clair que le Roi noir est en mesure de joindre n'importe laquelle de ces trois conjuguées. Et réciproquement trait aux Noirs, sur chacun de ces coups de Roi, existe une réplique adéquate.
Les cases e3 et c7 sont conjuguées. La case e7 ayant les mêmes propriétés, est aussi conjuguée de e3.
Depuis f3, on peut se rendre en e4 (conjuguée d8), f4 (conjugué d7), et e3 (conjuguée c7, nous venons de le voir). Il s'ensuit que c8, d'où le Roi peut de rendre en d8, d7 et c7, est conjuguée de f3.
Les cases f3 et c8 sont conjuguées. La case e8 ayant les mêmes propriétés (en remplaçant c7 par e7), est aussi conjuguée de f3.

|
|
|
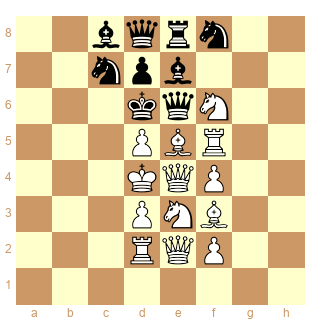
Considérez le diagramme surréaliste suivant :
Les pièces de même nature occupent des cases conjuguées. Ce "tableau" serait plus clair avec des pièces féeriques : par exemple, e7 est à la fois conjuguée de e5 et de e3 ! Mais j'espère qu'il vous aidera tout de même.
Sont conjuguées : f6/f8, e5/e7, d5/d7, f5/e8, e4/d8, f4/d7, e4/e6, d4/d6, e3/c7 et f3/c8. Enfin, les deux dernières conjugaisons, jointes à d3/d7, nous donnent e2/d8.
|
|
|
Dans l'affirmative, vous comprendrez aisément pourquoi, dans notre diagramme de base, que nous redonnons :
Les Blancs gagnent (K. Ebersz, 1935).
… il faille se méfier des principes : le coup naturel 1. Re2? (naturel car le Roi est sur la même colonne que e8, éloigné d'un nombre impair de cases) échoue sur 1...Rd8!!
… Et qu'il faille au contraire jouer le coup paradoxal 1. Rd2!! pour seulement sur 1...Rd8 jouer 2 Re2!!.

|
|
|
La solution enfin
1.Rd2!!
Etonnant à première vue. [1.Re2? Rd8!! 2.Rf2 (2.Rd2 Re8) 2...Rd7! 3.Re3 Re7 (3...Rc7 4.Re4 Rd8! ou 4.Rf4 Rd7!) 4.Rf3 (4.Re4 Re6 ou 4...Rd8) .Rd6 (4...Re8 5.Re4 Rd8! 6.Rf5 Re8!) 5.Rf4 Rd7! 6.Re5 Re7! 7.Rd5 Rd7 8.Rc4 Rd8 (8...Rc6) 9.Rb5 Rc7 10.Ra6 Rc6 11.Ra7 Rc7 12.Ra8 Rc8=]
1...Rd8 [1...Rd7 2.Rd3 Rc7 3.Re3]
2.Re2!! Rc8
[2...Re7 3.Re3 Re8 4. Rd4! Rd8 5. Re4!; 2...Rd7 3.Rd3 Re7 4 Re3]
3.Rf3!! Rc7 [3...Rd7 4.Rf4 Re6 5.Re4]
4.Re3! Retrouvant la règle du "rectangle impair"...
4...Rc8 5.Rd4!! Pas pour longtemps : e4 est interdite. [5.Re4? Rd8!! 6.Rf5 Re8!; 5.Rd3? Rd7! ; 5.Rf4? Rd7!]
5...Rd8 [5...Rd7 6.Rd5] 6.Re4!! Rd7 [6...Re8 7.Rf5] 7.Rd5 Re7 8.Rc6 [8.Re5 Re8 9.Rd6] 8...Re6 9.Rxb6 Rf5 10.a5
Les éclaircissements supplémentaires, remarques ou critiques seront les bienvenus. Amusez-vous bien.
|
|
|
Merci erony !
|
|
|
Je vous en prie
Une petite rectification : à 18h24, j'avais oublié que ...f6 est contré encore plus simplement par g6!.
|
|
|
Diagrammes saccagés.
20/08/2009 - 13:39 4k3/5p1p/1p5P/6P1/P7/8/8/4K3
23/08/2009 - 18:11 5k2/5p1p/1p3K1P/6P1/P7/8/8/8
23/08/2009 - 18:12 8/4kp1p/1p5P/4K1P1/P7/8/8/8
23/08/2009 - 18:14 8/3k1p1p/1p5P/3K2P1/P7/8/8/8
23/08/2009 - 18:15 4k3/5p1p/1p5P/5KP1/P7/8/8/8
23/08/2009 - 18:18 3k4/5p1p/1p5P/6P1/P3K3/8/8/8
23/08/2009 - 18:24 8/5p1p/1p2k2P/6P1/P3K3/8/8/8
23/08/2009 - 18:46 8/2k2p1p/1p5P/6P1/P7/4K3/8/8
23/08/2009 - 18:51 les cases conjuguées sont explicitées dans le texte au-dessous du "diagramme surréaliste".
23/08/2009 - 18:55 4k3/5p1p/1p5P/6P1/P7/8/8/4K3
Erony köszönöm -- Kornel kérem.

|
|
|
Je réalise que les diagrammes abîmés ont été réhabilités (merci les modos). En revanche, la plupart des titres ont tout bonnement disparu, ce qui rend l'exposé ci-dessus incompréhensible (pas merci les modos).
Les cases conjuguées, expliquées pour les nuls par erony le 20-08-2009 à 13:39
C'est parti par erony le 23-08-2009 à 18:11
Même question par erony le 23-08-2009 à 18:12
Même question par erony le 23-08-2009 à 18:14
Considérez à présent cette position par erony le 23-08-2009 à 18:15
Les cases f5 et e8 sont conjuguées. Posez maintenant le Roi blanc en e4 par erony le 23-08-2009 à 18:18
Toujours avec le RB en e4 par erony le 23-08-2009 à 18:24
Voyez maintenant ce diagramme par erony le 23-08-2009 à 18:46
Résumé des cases conjuguées par erony le 23-08-2009 à 18:51
Avez-vous bien suivi ? par erony le 23-08-2009 à 18:55
Bonne, quoique cahotique, lecture. Et bonne nuit.
|
|
|



