|
| Nombre de positions légales aux echecs par BoisColombes le
[Aller à la fin] |
| Actualités | |
Bonjour, je me demandais si cette méthode pour chercher le nombre de positions légales aux echecs pourrait être valable:
-Chercher le nombre de positions totales si toutes les positions étaient légales (à mon avis ça devrait être possible)
-Puis regarder sur un échantillon de positions prises au hasard relativement important quel pourcentage de positions sont des positions légales.
Est-ce qu'il existe un logiciel qui ferait cela?
Est-ce que ça a déja été fait?!
|
|
|
C'est tout à fait possible, (mais ça ne donne qu'une estimation)! c'est une illustration de la loi des grands nombres si je ne me trompe pas, et on pourra connaître l'incertitude de cette estimation à l'aide du théorème limite central.
Calculer le nombre de positions totales est quant à lui un problème de combinatoire très simple je pense.
|
|
|
Pas con ! Mais sans doute difficile à mettre en œuvre D'une part, je ne connais pas de logiciel permettant de vérifier rapidement la légalité.
D'autre part le pourcentage de positions réellement légales doit être très faible, donc il faut sans doute un grand échantillon pour obtenir quelque chose de significatif.
Pour le logiciel, ce n'est peut-être pas si dur que ça. Puisqu'on n'a pas à se préoccuper du nombre de coup (comme avec Natch ou Euclide), il suffit peut-être de se concentrer sur les stragtégies.
|
|
|
le nombre de position totales ne pose pas de problèmes, effectivement il ne peut jamais y avoir plus de 32 pièces sur l'échiquier (meme après promotion puisque ca prend la place d'un pion)
donc je pense qu'il suffit de faire 32 parmi 64 + 31 parmi 64 + 30 parmi 64 etc jusqu'a 2 parmi 64 (les 2 rois)
. Ca, c'est le nombre de positions totales. (je pense, dites moi si j'me trompe ! )
Oui, je sais, la dedans y'a aussi les positions ont les pions blancs sont sur la rangée 1 et les pions noirs sur la rangée 8, mais c'est pas grave parce qu'au fond le problème c'est de toruver le nombre de positions légales donc augmenter le nombre de positions illégales ne pose pas de pb....
Après, faut qu'un logiciel soit capable de déterminer si une position est légale ou pas.. Et ca, je suis pas sur que ca existe, si ?
|
|
|
ok mon calcul de position totale est complètement ridicule, oubliez moi :D
|
|
|
@Bois Colombes c'est ton entrainement pour Montlucon?
:-)
|
|
|
ok pour améliorer ce raisonnement il faut séparer chaque pion et les pièces. Chaque pièce peut aller sur 64 cases. En revanche le pion a n'a accès qu'à 21 cases, le pion b 26 cases, le pion c 30 cases et le pion d 32 cases
|
|
|
mais on entre déjà là dans le traitement de la légalité des positions ...
|
|
|
En théorie ça marche Ce n'est jamais qu'un sondage, si on arrivait à automatiser la procédure on pourrait même tirer des millions de positions mais :
- Compter le "nombre de positions totales" ça nécessite de savoir de quoi on parle. Ce n'est pas grave si ces positions incluent les cas où les pions sont en première rangée, mais le dénombrement reste très difficile pour deux raisons au moins :
-- les pions peuvent se promouvoir ce qui mulitplie le nombre de positions possibles (d'une manière qui n'est pas évidente de chiffrer)
-- surtout, il ne faut pas compter deux fois la même position, et c'est un problème de dénombrement particulièrement velu (si on se base sur la méthode d'adrct, chaque position apparaîtra plusieurs fois, mais ce ne sera pas le même plusieurs selon le matériel présent !)
Enfin, il n'est pas évident de déterminer la légalité d'une position automatiquement, on pourrait toutefois établir des règles qui élimineront une grand part des cas :
- pas de pions sur les 1ere et 8eme rangée
- pas d'échec si le camp n'est pas au trait, pas d'échec triple, d'échec par deux pions etc.
- pas plus de pions doublés que de pièces manquantes dans le camp adverse
- pas plus de pièces promues que possibles avec la matériel présent (plus compliqué à déterminer, mais avec les 32 pièces par exemple, aucune promotion possible, avec 31 pièces maximum deux pièces promues, ah non, trois... bin c'est pas facile)
|
|
|
Il semble que si on place les pièces et pions n'importe où (sur ou en dehors de l'échiquier) sans se préoccuper des règles, il y ait entre 10^53 et 10^54 possibilités. Cependant je suppose ici que toutes les pièces sont distinctes ce qui n'est pas le cas.
|
|
|
pessoa c'est pas si dur :
- 1er cas : on a les 32 pièces sur l'échiquier. 64 possibilités pour la première x 63 pour la seconde x ... c'est à dire 64!/32!
- 2nd cas : on a 31 pièces sur l'échiquier. 64 possibilités pour la première x 63 pour la seconde x ... c'est à dire 64!/33!
... Ca donne 5 . 10^53. Cependant on compte plusieurs fois la même position puisqu'on suppose implicitement que chaque pièce est différente (par exemple peu importe que ce soit la tour initialement en h1 ou a1 qui soit en c3 et l'autre en g3 ou le contraire c'est la même position).
|
|
|
En tout cas 5. 10 ^53 semble un bon majorant des positions légales ou pas.
|
|
|
s'il existait vraiment un logiciel qui soit capable de déterminer en un micro seconde si une position est légale ou pas, alors pas la peine de se casser la tete, on lui met toutes les positions de 32 pièces et moins indépendament de la dite pièce (cad qu'on peut se retrouver avec 18 rois), ca donne un nombre total qui est (32 parmi 64)^12 (6 choix de pièces noires + 6 choix de pièces blanches) + (31 parmi 64) ^12
bref et a partir de la a mon avis rien qu'en prenant un p'tit milliard de milliard de position aléatoirement on devrait obtenir une ptite centaine de légale et ca devrait donner une première approximation.
Bon, après, le problème c'est que le logiciel qui dit si la position est légale ou pas en 1 microseconde il n'existe pas et n'existera jamais, c'est bien trop complexe..
On peut toujours faciliter la tache en réduisant le nombre de position totales (que 16 pièces blanches ou noires au maximum, qu'un roi de chaque coté et toujours un roi, que 10 cavaliers au max etc) mais bon ca va pas révolutionner le pb qui est a mon avis tp complexe.
|
|
|
ok j'ai oublié quelque chose ci-dessus : quand on a 31 pièces sur l'échiquier, il faut prendre en compte la pièce qui manque ce qui fait 10 possibilités (pion B, pion N, cavalier B, ...). Et ainsi de suite. Donc le nombre que je propose est faux.
|
|
|
(18 c'est une expression on peut s'retrouver avec 32 rois quoi bref quoiqu'il en soit la majoration de dan est bien meilleure)
|
|
|
(a non effectivement elle est fausse)
|
|
|
on s'retrouve donc avec 64!/32! + 64!/33! * 10 + 64!/34! *10^2 etc etc non ?
|
|
|
Adrct : oui c'est un majorant, mais il est encore plus grossier que je pensais car le 10^2 ... surestime largement le nombre de possibilités des pièces qui ne sont pas sur l'échiquier. Cependant, ça peut rester intéressant.
|
|
|
ca donne 7 . 10^53pas tellement plus que tout à l'heure ... De plus un minorant doit être assez facile à trouver également, il suffit de ne considérer que les positions légales ou pas à 32 pièces, ce qui fait 64 (roiB) x 63 (roiN) x 62 (DB) x 61 (DN) x (60 x 59 ) /2 (TB) x ( 58 x 57 ) / 2 x .... = 4.6 10^42
|
|
|
Hum effectivement Il y avait pas mal de contraintes auxquelles je n'avais pas pensé...logiciel quasi impossible à réaliser, détermination du nombre de positions totales plus compliqué qu'il n'y parait (j'avais pensé comme Maelbreizh que ce serait un problème d'analyse relativement simple ou du moins faisable mais c'est vrai que le problème des pions complique le calcul.)
@splash: De toute façon, les championnats de France jeunes, moins je m'entraîne, mieux je les reussis...
|
|
|
@dan je pense que notre calcul est faux.
Car, si, oui, au maximum on a 32 pièces.. Ces 32 pièces ne sont jamais les memes...
Ca peut etre les 32 pièces de départ, mais aussi que des cavaliers blancs au lieu des pions blancs etc..
Il y a toujours, au maximum 32 pièces, mais plein de possibilités possibles pas seulement pour le placement de ses pièces, mais leur nature également..
Le vrai nombre est a mon avis très très très largement supérieur a 10^53
|
|
|
bah de quoi tu te plains on sait déjà qu'il y a entre 4.6 10^42 et 7 10 ^ 53 positions légales ou pas ... De plus le calcul exact est faisable. Par contre pour les positions légales, c'est inaccessible
|
|
|
oui tu as raison ...
|
|
|
@dan en fait oui. On a majoré le nombre de positions possibles avec les 32 pièces de départ. Sans prendre en compte toutes les complications induites par les promotions.
|
|
|
Exact. Les promotions multiplient allègrement les positions possibles
|
|
|
Le lien qui suit peut aider :-)
A HREF="http://fr.wikipedia.org/wiki/Nombre_de_Shannon
">http://fr.wikipedia.org/wiki/Nombre_de_Shannon
|
|
|
Zut.. http://fr.wikipedia.org/wiki/Nombre_de_Shannon
|
|
|
J'ai lu, je ne sais plus où que le nombre de parties (pas de positions) possibles était de l'ordre de 10^180.
Arrabal dans "Fischer : Le roi maudit" mentionne 319x10^9 combinaisons possibles après 4 coups, et 17x10^28 après 10 coups.
|
|
|
tout n'est pas perdu cependant car une promotion implique qu'il y a 31 pièces au maximum sur l'échiquier et on perd grosso modo un facteur 60. Pas sûr que le nombre de positions totales augmente beaucoup du coup, mais j'ai pas le temps de regarder maintenant.
|
|
|
dan et ar
|
|
|
oups moi et mes gros doigts !
dan et adrct, oui votre calcul et faux, pour une raison que j'ai citée et que dan31 a mentionnée également : par cette méthode, vous comptez une même position plusieurs fois.
Avec 32 pièces exactement, ça reste gérable. On a 6 paires de pièces interchangeables et deux octuplets de pions, également interchangeables. Chaque position apparaît donc 2^6x(8!)² fois, soit environ 104 milliards de fois. Restent 4,6x10^42 positions différentes. Bon
Avec 31 pièces, c'est déjà mortel. Certaines positions apparaissent 2^6x(8!)² fois (s'il manque une dame... ou un roi), d'autres 2^5x(8!)² fois (s'il manque un C, une T un F), d'autres 2^6x8!x7! fois (manque un pion).
Dès qu'on ajoute une promotion, la difficulté enfle car on va retomber sur des positions qu'on a déjà vues ("plusieurs" fois), d'autres qui sont nouvelles. Et on peut avoir jusqu'à trois promotions possibles (mais pas n'importe comment non plus). Je pense que laborieusement, on peut s'en sortir, en détaillant des litanies de cas.
Mais en descendant à 30 pièces et, si je ne m'abuse, jusqu'à 6 promotions envisageables... Amusez-vous !
|
|
|
Le problème se complique de par le fait q'il est possible qu'une position ait l'air dans un premier temps légal (i.e pas de pions sur les 1ère/8ème, pas d'echecs des deux rois en même temps), mais qu'il n'existe pas de parties permettant de parvenir à la position, i.e qu' il n'y ait pas de position à une analyse rétrograde partant de cette position.
Ce que je vois comme solution serait de tester toutes les parties possibles (en coupant chaque branche de l'arbre à la première répétition possible), et rentrer les positions nouvelles dans un tableau.
Heureusement cette solution n'est pas possible, sinon le jeu d'echecs serait résolu !
|
|
|
@foxi@pessoa l'objet avec dan n'était pas de ne compter que des positions légales, mais des positions tout court et de trouver un majorant "raisonnablement petit" (parce que c'est sur que 10^10000 est un majorant..). Donc ce n'est pas bien grave de compter quelques positions plusieurs fois ou d'y mettre des illégales. Le but de BoisColombes est de mettre toutes les positions possibles et après en tirer un gros nombre (mais qui sera qu'une petite proportion de l'énorme nombre que sera le majorant)et tester la légalité de ces positions choisies aléatoirement pour pouvoir déterminer la proportion de positions légales sur toutes les positions possibles, et donc déterminer approximativement le nombre de positions légales.
2 problèmes : le nombre de positions possibles est ahurissant
-il n'existe pas de logiciels déterminant la légalité de la position est quand bien meme il existerait il serait lent par rapport a ses chiffres astronomiques.
|
|
|
@foxi@Adrct @foxi
Effectivement le fait qu'une position puisse sembler légale mais ne provienne d'aucune partie légale complique vraiment le problème.
@Adrct
En fait ce n'est pas grave d'analyser qu'une petite proportion : en stats, pour calculer l'intervalle de confiance d'une proba, ce qui compte est le nombre d'évaluations, et pas la proportion du nombre total de possibilités.
Par exemple, un sondage pour un 2e tour d'élection présidentielle commence à être vraiment pas mal après 2000 personnes interrogées (si les personnes sont vraiment tirées au sort, ce qui est difficile), bien que 60 millions - 200 personnes n'aient pas été interrogées...
|
|
|
J'avais bien compris Le problème n'est pas que le nombre de positions "possibles" est ahurissant, le problème est que ce nombre est extrêmement difficile à calculer. Même à majorer autrement qu'avec un facteur 10^6.
Et je ne parle pas ici de positions légales, en effet. Si on avait le nombre de positions "possibles" et un moyen d'en générer aléatoirement + un testeur automatique qui ne se trompe pas trop, effectivement la méthode proposée par Boiscolombes serait correcte.
|
|
|
Améwi les promotions j'avais oublié les promotions. Ca doit être parce que je joue tellement mal en ce moment que j'amène rarement un pion sur la huitième...
Elles rendent effectivement le problème bien plus compliqué. Par contre, pour ceux qui ont lu le lien que j'ai posté, l'étude a déjà été faite apparemment: "le nombre de positions légales possibles est estimé entre 10^43 et 10^50." Estimation qui a forcément du induire une majoration et une minoration du nombre de positions possibles (pas forcément légales).
|
|
|
Pour ce qui est connu de ce problème... Je vous invite à visiter
< a href="http://wismuth.com/chess/chess.html">le site de François Labelle qui est un incontournable!
Sinon je rejoins l'avis de mon ami Axel (pessoa) en ce qui concerne la difficulté d'estimer le nombre de positions totales, sachant que les pions peuvent se promouvoir, qu'il y a deux Tours qui rendent des positions identiques avec les méthodes de dénombrement triviales... Je vous rappelle que la méthode proposée au départ demande la connaissance de deux nombres, déjà qu'avec un nombre imprécis ce sera sujet à caution, alors avec deux...
Enfin dernier écueil, les deux seuls programmes de résolution rétro que je connaisse sont Retractor qui résoud peu de problèmes (mais est impressionant tout de même) et Michel C.d qui est capable de résoudre tout problème rétro mais qui buggera sans doute devant l'ampleur de la tâche (pardonne mon "humour" Michel...).
|
|
|
le site de François Labelle
|
|
|
bon beaucoup de choses ont été dites, en particulier sur le cas à 32 pièces. Effectivement quand le nombre de pièces décroît, ça devient coton à cause des promotions. ET c'est faisable peut-être pour 31 et 30 mais ça devient un boulot ou au moins un hobby. Bref ... Peut-être pour 31 pièces, c'est assez accessible.
Autre chose qui nous aide peu mais intéressant par ailleurs : avec 32 pièces, les pions sont sur leurs colonnes d'origine donc chaque "duo" de pions (pions a blanc et noir) n'a que 15 positions possibles. Ce qui fait 15^8 façon de placer les 16 pions. Ensuite, on place les rois et les pions éliminent 24 possibilités (16 emplacement et au moins 8 contrôlées). Donc on a 15^8 x 40 x 40. Reste 46 cases pour les 14 pièces restantes. Donc sans se poser de questions 46 ! / (32 ! 2^6 ) le 2^6 pour les 6 duos de pièces identiques. Ce qui ne fait plus que 10 ^ 33 possibilités maximum avec 32 pièces sur l'échiquier alleluiah.
|
|
|
intéressant Abrobecker, en particulier on semble connaître le nombre de positions légales à 4 zeros prêt (entre 10^43 et 10^47 selon wiki)
|
|
|
Le cas 32 pièces me rappelle... Un programme réalisé quelques années en arrière et qui trouvait ce genre de bestioles:
Alain Brobecker, 2007/01/23
Tangente Jeux & Stratégies n°23 (v)
7K/2B2N2/8/P7/1PNPPP2/2P2R1P/BQ2R1P1/8
B:Rh8,Db2,Te2,Tf3,Cc4,Cf7,Fa2,Fc7,a5,b4,c3,d4,e4,f4,g2,h3/N:
16+0: Ajouter les 16 pièces noires pour une position légale sans pièce attaquée.
Bon ici c'est un sous ensemble de ce dont on parle, mais les temps de calcul, liés au nombre de positions, étaient déjà prohibitifs .
|
|
|
déjà si on choisit 32 cases vides : C(32,64)
on place les Rois : 32 * 31
pour le reste on choisit une pièce (B ou N) ou le vide : 9^30
c'est inférieur à 10^50.
|
|
|
ah j'ai oublié le peon. ça fait du 10^51 en fait
|
|
|
du 52 même bref, c'est mauvais.
|
|
|
En suivant les liens du site de François Labelle on tombe sur cette page: John's Chess Playground. D'après eux il y a moins de 2^155~10^47 positions.
La page rappelle aussi qu'il faut définir plus finement ce qu'est une position. Ainsi pour RBe1+TBh1 les positions doivent être comptées deux fois à cause de la possibilité de roquer ou pas. Il y a le même problème pour les prises en passant. Et bien sûr il faut parler du trait (certaines positions sont légales si c'est au noir de jouer mais pas si c'est au blancs...).
|
|
|
pas forcément si mauvais que ça dans l'idée en tout cas, car raisonner par case est plus efficace, ça donne C(64,32) x 32 x 31 x 10^30 c'est ça ?
|
|
|
11^30 hélas pion blanc ou noir
|
|
|
11^30 en fait (pour chaque cas, à choir parmi 5 pièces blanches, 5 noires et le vide).
Ca doit faire 3 x 10^52 ce qui n'est pas si mal sachant que ça me semble un majorant rigoureusement prouvé.
Intéressant le lien proposé par Alain (je venais de tomber dessus par le même chemin). Et on rappelle en effet que la simple notion de "position" n'est pas si évidente : François Labelle différencie le "diagramme" (la position des pièces sur l'échiquier) et la position (le diagramme plus d'autres infos, trait, possibilités de roque ou de pep, voire le nombre de coups selon la règle des 50 coups, passé de la position pour la règle des 3 répétitions)
|
|
|
croisement
|
|
|
alors en reprenant l'idée d'elkine mais en incorporant notre connaissance du cas à 32 pièces, on peut choisir 33 cases vides, ce qui doit améliorer les choses, en particulier on a du 11^29
|
|
|
avec 32 pièces, 5 . 10 ^ 42 diagrammes maximum. Avec 31 pièces ou moins C(64,33) x 31 x 30 x 11 ^29 diagrammes (on peut gratter 10 % mais c'est mesquin en plaçant d'abord les rois selon les positions légales). J'obtiens 2,6 10^51
|
|
|
J'essaye pour 32 pièces sur l'échiquier Pour chaque colonne 7+6+5+..+1=28 positions possibles des pions. Soit 28^8 pour les 8 pions.
Ensuite on regarde tous les arrangements de 16 cases parmi les 48 restantes sur lesquelles seront placées les pièces restantes dans un certain ordre (par ex RB,RN,DB,DN...), soit 48!/(48-16)!. Il reste à tuer l'ordre des Tours, Fous et Cavaliers (diviser par 2^6 je crois?). Et à multiplier par 2 pour le trait...
28^8×48!÷((32!)×2^5)=556995021550865603245530182320128000 ~10^36
Euh, où est la faille?
|
|
|
Exact dan On tombe à 2,8x10^51 sauf erreur. Ca avance bien.
|
|
|
Ah oui erreur J'avais oublié qu'il n'y a plus que 31 et 30 positions pour les rois.
|
|
|
Avec 31 pièces ça devient le b... Une pièce capturée peut permettre jusqu'à 3 promotions (si on a capturé un pion avec un autre pion)!
|
|
|
ref abrobecker pour les pions j'ai seulement 15^8, car chaque duo de pions (pions a blancs et noirs par exemple) n'a que 15 positions possibles.
|
|
|
Lire plus haut: [...]Soit 28^8 pour les 8 colonnes.[...]
|
|
|
ref abrobecker par ailleurs dans le cas 32 pièces, on peut démontrer que les pions de chaque camp contrôlent au moins 8 cases, donc il ne reste après avoir placé les 16 pions que 64 - 16 - 8 places disponibles pour chaque roi.
|
|
|
@dan31: tu as raison Je faisais partir mes pions blancs de a1 et les noirs de a8... ;)
|
|
|
oui et moi je dis 15^8. PAr exemple pour les pions a : a2/a7 - a3/a7 - a4/a7 ... compte les ca ne fait que 15.
|
|
|
croisement sorry
|
|
|
@ abrobecker voir mon post du 21h32, j'arrive à 10^33 possibilités pour les 32 pièces sur l'échiquier.
|
|
|
Je reessaye pour 32 pièces sur l'échiquier Pour chaque colonne 5+..+1=15 positions possibles des pions. Soit 15^8 pour les 8 colonnes.
Ensuite on regarde tous les arrangements de 16 cases parmi les 48 restantes sur lesquelles seront placées les pièces restantes dans un certain ordre (par ex RB,RN,DB,DN...), soit 48!/(48-16)!. Il reste à tuer l'ordre des Tours, Fous et Cavaliers (diviser par 2^6 je crois?). Et à multiplier par 2 pour le trait...
15^8×48!÷((32!)×2^5) = 3778480064138827327330050000000000 ~ 10^34
Euh, où est la faille?
|
|
|
pas de faille c'est à peu près ça, sauf que tu peux gratter quelques possibilités pour les rois 540 au lieu de 48) quand tu as placé tes 16 pions (cf post de 22h38)
|
|
|
lire ...quelques possibilités pour les rois (40 au lieu de 48) ...
|
|
|
@pessoa ton commentaire de 22h34 : c'est peut-être là qu'il faut douloureusement calculer le cas 31 pièces pour gagner encore un peu et appliquer l'idée d'elkine à 30 pièces.
|
|
|
Merci dan31! J'ai répété ce que tu as dis... ... avec des erreurs! ;p
Mais je suis pas encore convaincu par le contrôle des pions. Seul le double échec est pénible, le simple échec au roi par un pion ne l'est pas (sauf si le pion n'a pas bougé). Enfin tu n'avais pas compté le trait.
|
|
|
Autrement dit pour le contrôle des pions... Si le RB est en échec, on enlève 8 cases au RN, mais autrement le RN à le droit d'être en échec.
|
|
|
Petite coquetterie J'améliore la méthode elkine-dan de manière insignifiante en plaçant les rois avant les 33 cases vides.
3612 positions des rois sur des cases non contiguës.
Reste C(62,33) façons de placer les 33 cases vides.
Et 11^29 pour tout le reste.
Je multiplie le tout et je suis à 2,3x10^51 diagrammes.
|
|
|
eh bien disons que la prise en compte du trait permet au moins de passer pour un des rois de 48 à 40 possibilités (celui qui n'a pas le trait ne peut pas être échecs). Pour l'autre tu as raison, il reste à 48. Mais de toutes façons, c'est annexe par rapport au problème total avec nombre de pièces quelconques. En effet, on a prouvé qu'on peut ignorer le cas 32 pièces car le nombre de positions est négligeable par rapport à nos majorations dans les autres cas.
|
|
|
oui pessoa, je l'avais du reste mentionné à 22h32, on peut gagner 10% en plaçant les rois avant (3612 possibilités au lieu de 64 x 63)
|
|
|
Avec 34 cases vides On descend à 1,8x10^50.
On doit pouvoir montrer en comptant à la truelle que le nombre de positions avec 31 pièces est négligeable devant ce chiffre, mais je doute qu'on puisse encore enlever une pièce sans souffrir.
|
|
|
bon on est tous d'accord il y a juste moult croisements et lecture parfois rapide des autres posts. Je vais me reposer un peu, j'espère que demain vous aurez bien progressé. En particulier pessoa me semblait avoir des idées pour le cas 31 pièces (tu parlais de 3 promotions maximum ?)
|
|
|
Pause aussi 3 promotions maximum avec 31 pièces, par exemple pion a blanc prend b noir, va a promotion. Le "vrai" pion b blanc va aussi à promotion en b8 et le pion a des noirs en a1.
En ce cas on a jusqu'à 19 pièces (10 d'un camp, 9 de l'autre) et 12 pions (6 de chaque côté).
Si la prise est celle d'une pièce, ça fait une promo de chaque côté donc 9 pièces contre 8 et 7 pions chacun.
Enfin avec pièce x pion, une seule promo possible donc in fine là aussi 9 pièces contre 8 et 7 pions de chaque côté.
Il faut ajouter les cas où les promos potentielles n'ont pas lieu, finalement ça ne fait tant de cas à énumérer sachant que les pions qui restent sont forcément face à face, il reste à lister des cas fastidieux selon la nature des promotions mais on a finalement n cas analogue au problème à 32 pièces, avec n qui ne doit pas trop s'envoler.
Sans trop fignoler, on doit avoir un n pas trop monstrueux, de sorte qu'en le multipliant par 10^33 on doit encore être loin de notre majorant 10^51 pour tous les cas jusqu'à 30 pièces.
|
|
|
Quelqu'un a-t'il regardé ce que donne les tables de finales jusqu'à 6 ou 7 pièces. Je ne pense pas qu'ils puissent traiter tous les cas d'illégalités, mais pour RB+TB/RN on obtient:
121564 positions illégales
402724 positions legales
93.6% mats et 6.4% nulles.
|
|
|
Hummm.... On oublie, même avec 7 pièces ça semble trop petit.
|
|
|
@pessoa Tu dois avoir raison, le cas 31 pièces doit être également relativement négligeable. Intuitivement cela semble le cas. J'ai fait un peiti calcul qui donne un indice. J'évalue juste le cas 31 pièces avec 3 promotions, qui paraît fournir le nombre le plus élevé de possibilités car les pièces ont plus de cases possibles que les pions.
Dans ce cas, on a forcément 1 prise de pions comme tu l'as dit par exemple une partie commençant par 1.a4 a5 2.b4 b5 3.axb5 et les pions blancs a et b se promeuvent ainsi que le pion a noir. On reste donc avec 6 duos de pions : en effet, n'oublions pas que d'autres prises ne sont pas possibles car on a 31 pièces.
Je place les 6 duos de pions, ça donne 15^6 comme déjà détaillé. Puis les 2 rois 3612 au maximum. Je fais la suite à la elkine : les 33 cases vides sur 50 restantes : C(50,33). Les 17 pièces restantes qui ne sont ni des pions ni des rois ni vides : 8^17. Je multiplie le tout et obtient 10^39.
Les autres cas à 31 pièces (2 promotions, 1 promotion ou 0 promotion) doivent donner un nombre moins élevé. Bref je reste amplement en-dessous de 10^50. Maintenant il faut changer de technique à mois de vouloir se taper un boulot de fou. J'ajoute qu'il reste des détails (trait, droit au roque, prise en passant) mais que ça ne sert à rien de les prendre en compte si on ne peut obtenir quelque chose d'assez précis d'autre part. En particulier, je suis assez curieux de savoir comment le minorant de 10^43 pour le nombre de positions légales donnés sur wiki a été trouvé, si jamais il ne s'agit pas d'une simple affirmation sans fondement.
|
|
|
un sujet à proposer dans une université traitant de ce domaine des maths?
|
|
|
Pour le jeu de Go c'est plus facile c'est environ 361! (!=factoriel pour les non mathématiciens. ex: 5!= 5x4x3x2x1). Hélas cette méthode ne marche pas pour les échecs car le nombre de réponse dépend du coup précédant.
|
|
|
Je remonte ce fil (qu'on pourrait d'ailleurs reprendre) pour y poser une devinette qui ne fait pas avancer le schmilblick : combien y a-t-il de positions légales avec 32 pièces et sans qu'aucun pion n'ait bougé de sa case initiale ? J'obtiens 28 627 830, avec prise en compte du trait et du droit au roque.
|
|
|
et d'ailleurs ce nombre est inexact je viens de m'en apercevoir.
|
|
|
pour le droit au roque , si les fous n'ont pas bougé , la question est résolue
...
en fait , ce que je dis doit être une anerie
|
|
|
il s'agit du droit au roque potentiel : par exemple, deux diagrammes identiques avec Re1 et Ta1 peuvent être deux positions différentes selon que la tour ait déjà bougé ou non. Et comme les cavaliers peuvent bouger, les tours le peuvent aussi.
|
|
|
Je trouve 82 200 096 et ce n'est déjà pas simple de tout prendre en compte (d'ailleurs j'ai peut-être oublié des choses).
|
|
|
Ca fait loin de mon calcul, qui est faux, mais si mon raisonnement n'oublie rien, il n'est pas faux de beaucoup.
Le principe : il y a 2 positions possibles par tours soit 16 positions en tout. Avec la prise en compte des droits au roque, ça fait si je ne me trompe 81 possibilités.
Ensuite on place les cavaliers, il reste 36 places libres donc C(36,2) pour les blancs et C(34,2) pour les noirs. 81 x C(36,2) X C(34,2) = 28 627 830.
Grâce à des considérations de parité, pas la peine de prendre en compte le trait, la position des pièces le détermine.
Par contre, j'ai oublié d'enlever tous les cas où plusieurs cavaliers donnent échec, ainsi que les cas où un cavalier donne échec mais où ce n'est pas en accord avec les considérations de parité qui déterminent le trait.
|
|
|
Ok, j'avais oublié la parité et je m'étais par ailleurs planté dans la réalisation du calcul. Mais j'avais réfléchi aux questions d'échecs.
Reprenons :
81 possibilités pour la position des tours + les droits au roque : OK.
Pour le camp au trait, les deux cases qui donnent échec sont interdites aux cavalier, donc il reste C(34,2) cases libres.
Pour le camp adverse, seul l'échec avec les deux cavalier est prohibé, donc C(34,2)-1 possibilités.
Effectivement la parité implique qu'on connaît le trait (présenté comme cela il y a un petit raisonnement circulaire donc je ne suis pas sûr que ça reste 100% rigoureux, en fait).
Soit 81*561*560=25 446 960 positions légales.
|
|
|
Exemple tiré d'un livre de Hartston: pour avoir une partie au moins nulle, il suffit qu'on ait des pions sextuplés de sa couleur sur la colonne a ou h. En effet, ces pions auront effectué 15 captures, et la pièce restante ne pourra être que le Roi adverse, donc on tient au moins la nulle.
Bref, il faut tenir compte des pions!
|
|
|
ça dépend si c'est en cadence rapide et qu'on se trompe en faisant glisser le pion b sur la rangée a y a pas nul , à part si la dernière pièce qu'il nous reste soit un fou ou un cavalier , il me semble aussi qu'en partie lente si on se trompe et qu'on mange 3 fois le roi de l'adversaire on perd la partie, à confirmer
|
|
|
oui pessoa je pense qu'il y a un hic avec ta proposition pour le trait mais je n'en suis pas vraiment sûr. La façon dont je prenais en compte le trait était de dire : la position de l'ensemble des pièces suffit à déterminer le trait, donc ce n'est pas la peine de compter chaque position 2 fois pour trait aux blancs ou trait aux noirs. Donc je fixe la position et pas la peine de se préoccuper du trait.
Quand tu fixes le trait dans ta proposition, le nombre de possibilités pour les deux derniers cavaliers à placer est réduit car il doit respecter des conditions de parité. Enfin il me semble, c'est pas encore très clair pour moi. En effet, peut-être que des symétries entre le cas où les blancs font échec et celui où ce sont les noirs font que ça marche quand même.
J'ai un autre moyen de faire, cad retrancher les positions illégales de mon premier décompte. Mais là j'ai la flemme, je regarderai demain.
|
|
|
En fait c'est très subtil.
On peut l'étudier en deux fois.
1) Supposons les blancs au trait
Il y a alors C(34,2) possibilité pour place les deux cavaliers blancs (toutes les cases encore vides sauf d6 et f6).
Il y a ensuite C(34,2) possibilités pour placer les cavaliers noirs. Une de ces possibilités est à éliminer, les cavaliers en d3 et f3. Et la moitié environ des possibilité est incorrecte pour cause de parité. Mais il n'est pas du tout facile de se convaincre que la moitié exactement des positions restantes est incorrecte pour raison de parité.
En particulier parce dans les façons de placer les cavaliers blancs, il y a plus de noires que blanches...
|
|
|
A priori une erreur constante dans vos calcul : les cavaliers blancs et noirs peuvent se chevaucher, non ?
|
|
|
non Bellamy, on a compté 36 places pour les blancs et 34 pour les noirs, je me cite : "Ensuite on place les cavaliers, il reste 36 places libres donc C(36,2) pour les blancs et C(34,2) pour les noirs"
|
|
|
@Bellamy: "les cavaliers [...] peuvent se chevaucher"
Excellent.
|
|
|
Amusant : une position illégale que nous n'avons pas éliminée dans nos calculs.

|
|
|
exact le trait est aux noirs donc c'est impossible! Bien vu ! Tu aurais même pu en mettre un dans le camp des noirs (cavalier blanc a8 et noir b6).
Quant à moi je retranche facilement les positions illégales avec 4 échecs, 3 échecs ou 2 échecs. Mais pour celles avec un échecs mais trait dans le mauvais sens, c'est plus lourd. On pourrait dénombrer tous les cas mais l'intérêt est limité. J'ai pas trop envie de m'y coller.
Et il y a en plus les nouvelles possibilités que tu viens de trouver même si celles-ci doivent être peu nombreuses.
A la base j'avais une idée élégante mais il y avait cette question d'échecs.
|
|
|
Le droit aux roques peut aussi poser des problèmes :

|
|
|
bon on s'éloigne de la résolution de la question initiale et même de la possibilité de la résoudre facilement, mais ça devient marrant.
Si je ne m'abuse c'est trait aux noirs donc les blancs viennent de jouer une tour. Donc ce diagramme représente trois positions possibles (aucun droit au roque, droit au grand roque seulement, droit au petit roque seulement) et non pas 4 (droit aux 2 roques exclu).
Pour des analystes rétrogrades, c'est quasiment naturel de débusquer ces positions. D'autres idées ?
|
|
|
Ou plutôt 12 positions et non pas 16.
Difficile de trouver des problèmes très intéressants avec les conditions imposées.
|
|
|
"Ou plutôt 12 positions et non pas 16." Oui en effet, en prenant en compte le droit au roque noir, si c'est bien ce que tu veux dire.
Ce qui est amusant c'est que c'est le seul coin où ça semble marcher. A l'aile dame, il n'y pas échec avec un Cavalier en c6. Et du côté blanc, les conditions de trait font que ce serait aux noirs de jouer.
Cependant on peut compenser en mettant de ce cas une tour en b1 : dans le diagramme ci-après, les noirs viennent de jouer une tour, donc il n'y a que 3 possibilités pour le droit au roque noir et 2 pour le blanc (à cause de la tour en b1), ce qui fait 6 positions au lieu de 8.

|
|
|
Il y a aussi ce cas : le trait est aux blancs donc les noirs viennent de jouer une tour. Donc ce diagramme fait 3 positions au lieu de 4. Cette fois on ne peut inverser le diagramme il me semble

|
|
|
Selon mon ordinateur, la réponse à la devinette de dan31 est 25452174, qu'on peut séparer selon que le nombre de demi-coups est de la forme 4k+0, 4*k+1, 4k+2 ou 4k+3:
6420862 + 6360940 + 6306595 + 6363777 = 25452174
Pour les diagrammes, les nombres respectifs sont
1261146 + 1257132 + 1252700 + 1256618 = 5027596
Toutes les positions peuvent être obtenues en 14.5 coups ou moins, et tous les diagrammes peuvent être obtenus en 13.0 coups ou moins. Voici le seul diagramme qui demande 13.0 coups:

|
|
|
@dan31 : ok, j'avais mal lu un des calculs de pessoa.
@Flab : Super !
Il n'y a plus qu'à retrouver ces valeurs par calcul "humain".
|
|
|
intéressant en particulier le modulo 4 au lieu de la parité. Pas le temps d'y penser tout de suite d'ailleurs. Mais je jetterai un coup d'oeil demain. Combien de temps de calcul stp flab ?
Petit exercice : répéter l'opération avec les 15 puissances 8 positions possibles pour les pions lorsqu'il n'y a pas capture et générer ainsi le nombre de positions légales totales à 32 pièces. Non je déconne ! (Quoique ... en distribuant le calcul, ça ne fait que 2.5 milliards de cas à traiter, mais dans la plupart des configurations où les pions bougent, les pièces peuvent aller partout)
|
|
|
Evidemment s'il y avait une personne qui pouvait résoudre ce problème, c'était François ! Grand merci pour ce travail.
Je n'étais pas si loin avec mon calcul (quand même étonné que la bonne réponse soit légèrement supérieure et non inférieure)
Amusant aussi la position en 13 coups, enfin surtout son unicité.
|
|
|
Sinon pour la question de départ de BoisColombes :
Je me pose 2 questions, si quelqu'un a les réponses ...
1) Les meilleurs moteurs d'analyse d'echecs calculent combien de coups à la seconde ?
2) Laisser un moteur tourner à l'infini lui prendrait un temps infini pour tout calculer ou alors prendrait il que quelques jours ?
Si c'est pas trop long il donnerait le nombre de positions analysées.
Je suppose que sur Internet quelque part quelqu'un a déjà trouvé le nombre de positions possibles au total ?
|
|
|
Ah mais c'est vrai qu'en plus il y aurait des doublons c'est ca ? car la question etait le nombre de positions possibles legales et pas le nombre de coups
|
|
|
@dan31: Ça a pris environ 1 heure.
@pessoa: Dans ton calcul, "C(34,2)-1" est pessimiste. Il ne faut pas soustraire 1 si le camp au trait occupe l'une des 2 cases prohibées.
|
|
|
@Flab : merci. Sur mes 28 627 830 millions de positions totales possibles dont je suis à peu près sûr (comprenant des positions illégales), j'arrive à retrancher sans douleur les positions illégales avec 2,3 et 4 échecs. Mais si je ne me trompe pas, ça ne fait même pas 500 000 positions de moins. Il reste plus de 2 millions de positions illégales à retrancher pour arriver ton évaluation. Evidemment, les positions illégales avec 1 échecs sont plus complexes à prendre en compte, car on doit tenir compte du trait. Et il reste aussi à retrancher les positions pathologiques, proposées par pessoa, petiteglise et moi-même. C'est vrai que j'aimerais bien retomber sur la valeur que tu donnes, mais il faudra peut-être que j'écrive un petit programme pour traiter les cas à 1 échec, j'ai vraiment la flemme de la faire à la main.
@weakman : il y a environ 10 puissance 120 parties possibles et 10 puissance 45 positions possibles. Je ne suis pas sûr de bien comprendre ta question, mais les moteurs d'analyse calculent quelques millions de positions par seconde. Cependant, ils ne font pas que parcourir l'arbre des possibilités, ils passent aussi du temps à évaluer la position et à sélectionner les branches à explorer. Quoiqu'il en soit, le temps serait en effet infini (plus de 10 puissance 30 secondes, donc plus de 10 puissance 20 années). Et il y a bien sûr l'aspect mémoire, car il faut mémoriser toutes les positions pour ne pas y repasser deux fois.
|
|
|
@dan31: Quelle approximation ça donne si tu retranches les positions avec 2, 3 et 4 échecs, et la moitié des positions avec 1 échec?
Pour le nombre de parties possibles, c'est infini. Et même si on force les joueurs à demander la nulle quand ils le peuvent (comme dans le codex de composition), c'est facile de montrer que le nombre est beaucoup plus grand que 10^120, non?
|
|
|
@flab : j'en obtiens 25 452 225. Pas eu le temps de vérifier de près d'ailleurs et je viens de le faire à la hâte, mais ça semble pas anormal. C'est très légèrement supérieur à ton nombre et il reste à retrancher les positions pathologiques.
Par contre, je suis loin d'être sûr que le nombre de positions légales avec 1 échecs soit égal au nombre de positions illégales avec un échecs. Ca pourrait être le cas, mais si c'est vrai, ça m'échappe pour l'instant. Et si ce n'est pas le cas, ce chiffre de 25 452 225 resterait une approximation.
|
|
|
quoiqu'il y a quand même des histoires de symétrie par rapport aux 4e-5e rangées qui font qu'une position illégale peut avoir un miroir légal, si la position des tours ne l'empêche pas. A vérifier ! Si les tours sont toutes symétriques par rapport à cette ligne c'est clair que ça marche, donc diviser par 2 doit être au moins une très bonne approximation, mais je ne vois toujours pas l'égalité.
|
|
|
hum, après une petite réflexion ce matin, je pense obtenir une bijection entre l'ensemble des positions légales et illégales avec 1 seul échec. La certitude n'est pas absolue cependant, j'ai travaillé rapidement. Cela signifierait que 25 452 225 est le nombre de positions légales avant d'enlever les pathologiques.
On pourrait recenser ces dernières pour confirmer. Si je compte bien, pessoa en propose 4, petiteglise 4 (16-12), et moi 3. Cependant, on doit en rater : ainsi le diagramme de flab représente 2 possiblités de droit au roque et non 4.
Pour progresser, compter d'abord les diagrammes serait plus aisé : on enlève les notions de droit au roque, de prise en passant et de trait c'est cela ?
|
|
|
Oui le cas des diagrammes est plus simple. T'en obtiens 25452225 / 81 * 16 = 5027600, non?
Quand un cavalier fait échec, au moins une des 4 tours est capable de bouger et changer le trait. On choisit la première tour capable de le faire et on obtient une bijection entre diagrammes légaux et illégaux. Donc 5027600 est exact et pas une approximation.
Il faut maintenant expliquer les 5027600 - 5027596 = 4 diagrammes de trop. Je crois qu'il s'agit du diagramme de pessoa (le 26/11/2012 - 19:29:16) et de 3 autres diagrammes semblables.
|
|
|
@flab : je tombe sur mes pattes pour le nombre de diagrammes, mais est-ce que c'est juste ?
Je détaille :
16 possibilités pour les tours. Pour chacune d'entre elles, C(36,2) pour les cavaliers blancs et C(34,2) pour les cavaliers noirs, soit 5 654 880 diagrammes possibles, légaux comme illégaux.
On retranche les cas illégaux :
- on peut générer 4 diagrammes illégaux comme celui de pessoa, le 26/11/2012 - 19:29:16 : 2 en patant les cavaliers blancs et 2 en patant les cavaliers noirs.
- il y a 16 (positions des tours) cas avec 4 échecs.
- il y a 16 X 2 X 2 X 32 cas avec 3 échecs
(le premier 2 est pour le camp qui fait 2 échecs, le second pour la case d'où l'échec est fait pour l'autre camp, le 32 pour le dernier cavalier).
- il y a 16 x [ 2 X C(32,2) + 4 X (33+ 32 X 32)] cas avec 2 échecs.
(sans m’appesantir, le premier terme est le cas où le même camp donne les deux échecs et le second cas celui où les deux camps donnent chacun un échec).
Je détaille maintenant les cas avec un échec, légaux et illégaux : il y en a 16 X 4 X (2C(33,2)+32C(32,2)).
(le 4 pour la case d'échec, le 2C(33,2) pour le cas où le second cavalier du camp qui fait échec met aussi en "échec" son roi avec l'autre cavalier et l'autre terme pour l'autre cas).
J'établis une bijection entre les cas avec un échec légaux et illégaux, donc j'ai exactement la moitié de ce nombre de cas illégaux.
Ainsi, on a, parmi tous mes diagrammes 627 284 diagrammes illégaux. Que je retranche à 5 654 880 diagrammes possibles pour obtenir 5 027 596 soit la même valeur que flab !
EDIT : croisement avec ta réponse le temps que je rédige mon long post. D'accord pour la bijection
|
|
|
Je crois aussi avoir établi la bijection pour le cas des positions ce qui est moins simple car bouger une tour comme tu le proposes pour les diagrammes modifie les droits au roque.
Je procède par une symétrie par rapport au milieu de l'échiquier. On applique cette symétrie à la position des tours et des cavaliers (en changeant aussi la couleur de chaque pièce) : on ne modifie pas le trait et on a donc une bijection sans modifier le nombre total de droit au roque.
Si c'est juste, il reste 51 autres positions illégales à détecter, cf les différents diagrammes ci-dessus.
|
|
|
J'ai la liste (assisté par ordinateur). Il s'agit de 24 diagrammes que j'ai groupés en 5 catégories, dont une nouvelle catégorie que j'illustre à la fin.
1rbqkb1r/pppppppp/8/8/8/1n4n1/PPPPPPPP/NRBQKBRN : 2 - 0 = 2 (pessoa)
r1bqkbr1/pppppppp/8/8/8/1n4n1/PPPPPPPP/NRBQKBRN : 2 - 0 = 2
nrbqkbrn/pppppppp/1N4N1/8/8/8/PPPPPPPP/R1BQKB1R : 4 - 0 = 4
nrbqkbrn/pppppppp/1N4N1/8/8/8/PPPPPPPP/1RBQKBR1 : 1 - 0 = 1
r1bqkbNr/pppppppp/7N/5n2/6n1/8/PPPPPPPP/R1BQKB1R : 16 - 12 = 4 (Petiteglise)
r1bqkb1r/pppppppp/8/6N1/5N2/7n/PPPPPPPP/1RBQKBnR : 8 - 6 = 2 (dan31 #1)
r1bqkb1r/pppppppp/8/8/8/1N4N1/PPPPPPPP/nRBQKBRn : 4 - 3 = 1 (dan31 #2)
NrbqkbNr/pppppppp/1n5n/8/8/8/PPPPPPPP/R1BQKB1R : 8 - 6 = 2
nrbqkb1r/pppppppp/1N6/8/8/7N/PPPPPPPP/1RBQKBnR : 4 - 2 = 2 (Flab)
nrbqkb1r/pppppppp/1N6/8/8/1N6/PPPPPPPP/nRBQKB1R : 4 - 2 = 2
r1bqkbrn/pppppppp/6N1/8/8/1N6/PPPPPPPP/nRBQKB1R : 4 - 2 = 2
r1bqkbrn/pppppppp/6N1/8/8/7N/PPPPPPPP/1RBQKBnR : 4 - 2 = 2
nrbqkb1r/pppppppp/1N6/8/8/6N1/PPPPPPPP/R1BQKBRn : 4 - 2 = 2
r1bqkbrn/pppppppp/6N1/8/8/6N1/PPPPPPPP/R1BQKBRn : 4 - 2 = 2
r1bqkbNr/pppppppp/7n/8/8/1n6/PPPPPPPP/NRBQKB1R : 8 - 4 = 4
r1bqkbNr/pppppppp/7n/8/8/6n1/PPPPPPPP/R1BQKBRN : 8 - 4 = 4
1rbqkbrN/pppppppp/6n1/8/8/1n6/PPPPPPPP/NRBQKB1R : 2 - 1 = 1
Nrbqkbr1/pppppppp/1n6/8/8/1n6/PPPPPPPP/NRBQKB1R : 2 - 1 = 1
1rbqkbrN/pppppppp/6n1/8/8/6n1/PPPPPPPP/R1BQKBRN : 2 - 1 = 1
Nrbqkbr1/pppppppp/1n6/8/8/6n1/PPPPPPPP/R1BQKBRN : 2 - 1 = 1
r1bqkbrn/pppppppp/6N1/5N2/7n/8/PPPPPPPP/1RBQKB1R : 4 - 2 = 2
r1bqkbrn/pppppppp/6N1/5N2/7n/8/PPPPPPPP/R1BQKBR1 : 4 - 2 = 2
r1bqkb1r/pppppppp/8/7N/5n2/6n1/PPPPPPPP/R1BQKBRN : 8 - 4 = 4
1rbqkbr1/pppppppp/8/7N/5n2/6n1/PPPPPPPP/R1BQKBRN : 2 - 1 = 1
2+2+4+1 + 4+2 + 1+2 + 2+2+2+2+2+2+4+4+1+1+1+1 + 2+2+4+1 = 51
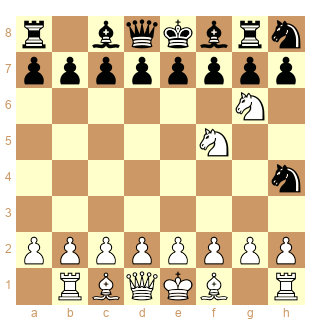
|
|
|
pas mal ce dernier cas-type. Ton programme fonctionne en explorant intégralement l'arbre jusqu'à retrouver une position déjà stockée ? Si c'est le cas il élimine les transpositions j'imagine.
Si c'est le cas, combien de positions peut-il traiter ? On arrive un peu aux limites avec ce problème j'imagine qu'on doit difficilement pouvoir dépasser un nombre de positions disons 10 fois supérieur ?
|
|
|
C'est pas difficile, juste long. Mon record c'est 85 milliards de positions au même ply lors de l'énumération de toutes les PJ en 5.0 coups. C'est 13000x plus que 6420862 pour ta devinette.
|
|
|
Je profite de cet article pour signaler que j'ai commis ce travail, qui permet de majorer le nombre de diagrammes possibles sans promotion par 4 fois 10 puissance 37 :
https://hal-univ-avignon.archives-ouvertes.fr/hal-03483904
La valeur est un peu anecdotique, d'autant qu'on ne prend pas les promotions en compte, mais il est possible que la méthode soit intéressante pour évaluer les structures de pions légales ou pas (aucune idée de ce que font les logiciels de vérification d'analyse rétrograde par exemple). D'autre part inclure la possibilité des promotions n'est pas conceptuellement très compliqué mais je ne sais pas si la puissance de calcul suivra.
|
|
|
Je remonte juste ce post pour poser une question aux utilisateurs voire aux concepteurs (on peut rêver) de programmes pour l'analyse rétrograde. Ces logiciels permettent-ils des vérifications un peu systématiques de la légalité de la structure de pions ? J'ai implémenté un tel système dans le manuscrit cité dans le post ci-dessus et je voudrais savoir ce qui se fait déjà par ailleurs.
|
|
|



