|
| Puzzle des diagonales paires par EricAngelini1 le
[Aller à la fin] |
| Problèmes | |
L'échiquier est en position de départ d'une partie orthodoxe — mais sans les Noirs. Quel est le minimum de coups consécutifs que Blanc doit jouer pour que toutes ses pièces soient sur des diagonales comportant un nombre pair de pièces ?
|
|
|
Ce petit puzzle ne soulève pas les foules. Expliquons mieux et appelons (sur le modèle des aiguilles d’une pendule) « 10:23 » les diagonales parallèles à la droite a8-h1 et « 13:37 » les diagonales parallèles à a1-h8.
En position blanche de départ, deux diagonales passent par le pion a2, une 10:23 (qui passe aussi par le Cb1), et une 13:37 (célibataire).
Trois autres « diagonales célibataires » sont présentes au départ, la 10:23 passant uniquement par la Tour a1, la 10:23 passant uniquement par le pion h2 et la 13:37 passant par la Tour h1.
Toutes les autres diagonales qui traversent au moins une pièce blanche passent par deux pièces blanches exactement (un nombre pair). Une diagonale ne traversant aucune pièce est dite « orpheline ».
|
|
|
Le diagramme de départ :

|
|
|
Dernier exemple ci-dessous : après 1. c2-c4 les deux diagonales passant par a2 comportent bien un nombre pair de pièces — mais la 10:23 passant désormais par la Dame n'en comporte plus qu'une (nombre impair), la 13:37 passant par le Cavalier b1 aussi, et la 10:23 passant par le Fou f1 idem (3 pièces).
Le puzzle consiste donc à disposer rapidement les 16 pièces blanches sur des diagonales paires.

|
|
|
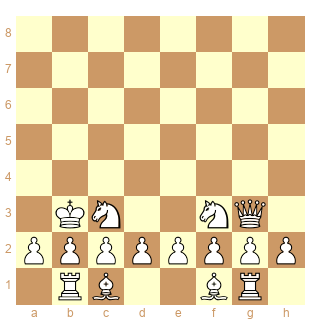
Pour terminer (?) voici une position qui convient aux diagonales, mais qui est illégale :
|
|
|
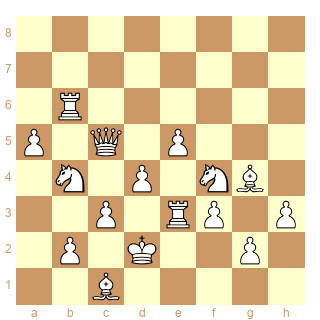
j'ai en 23 coups
1. e4 2. Qh5 3. Qc5 4. e5 5. Be2 6. Bg4 7. Ne2 Nc6
8. Nf4 9. d4 10. a4 11. a5 12. Ra3 13. Rb3 14. Rb6
15. Nc3 16. Na2 17. Nb4 18. c3 19. Kd2 20. Re1 Nb8
21. Re3 22. f3 23. h3
|
|
|
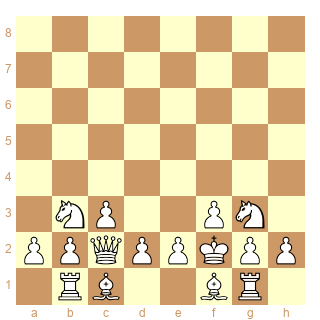
ou en 14, c'est mieux quand même
1. f3 2. Nh3 3. Nf2 4. Ne4 5. Ng3 6. Kf2 7. Rg1 Nf6
8. c3 9. Na3 10. Rb1 11. Nc2 12. Nd4 13. Nb3 14.
Qc2
|
|
|
en 11 coups si on intervertit les deux cavaliers avec le couple royal.
Mais où ai-je la tête ces derniers temps ?
|
|
|
Oui, j’ai cette solution à 11 coups — et une autre à 11 coups aussi avec un roque !
|
|
|



