|
| Un problème scaccographique amusant! par Abrobecker le
[Aller à la fin] |
| Problèmes | |
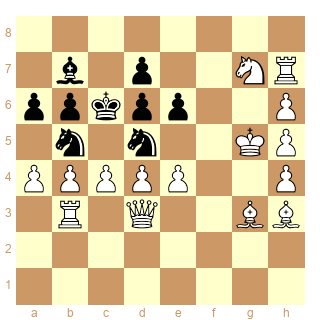
Je viens de découvrir ce problème de Andrew Buchanan et je l'ai trouvé très original et amusant. Donc je partage.
Son énoncé est: Saurez-vous résoudre ce problème sans que l'on vous donne l'énoncé?

|
|
|
Il me manque encore un petit bout d’AR (le fou de case blanche), mais l’idée est géniale !
Bel énoncé ;-)
|
|
|
Je crois que j’ai complété l’AR, mais la position me semble illégale, donc j’ai dû faire une erreur…
Le fou a forcément pris quelque chose en d6, non ?
[Édit] Ah non !
|
|
|
Bonjour Alain,
J'ai besoin d'un premier indice, est-ce que c'est un problème abordable, ou faut-il être expert pour le résoudre ?
|
|
|
Le dernier coup noir doit avoir été gxFh3. Non ?
|
|
|
à chemtov : je vous ai envoyé un mail (l'avez-vous reçu ?)
|
|
|
Oui, oui, bien sûr, désolé. Mais j'attendais, pour répondre, de... ranger chez moi et au club ( cela risque d'être long ! ). Images des locaux à peu près identiques à celle présentée ici dans ce problème ! Evidemment, si je fuis le travail en me réfugiant dans ce havre de paix et de sérenité qu'est FE, cela ne risque pas de s'arranger...
|
|
|
si l'on pouvait démontrer que le dernier coup noir fut ç7-ç5 le mat en 1 (PEP) serait sympa !
mais voilà, je n'y connais rien en scaccographie ...
|
|
|
Bien sûr, mais il faut pour cela que le fou ait pris quelque chose en d6. Hors il semble que les pions blancs ont déjà pris dix fois. Non ? Mais je me demande où est passé le pion a7... Aurait-il pris le fou en b5 ? (donc pas de gxFh3).
Zut, supergogol m'a culpabilisé... il faut que j'aille bosser un peu.
++
|
|
|
Les pions blancs ont pris neuf fois, c’est-à-dire toutes les pièces noires manquantes sauf le pion b (le pion b2 vient de la colonne a).
Mais j’espère que vous n’êtes pas passé à côté de l’énoncé !
|
|
|
Et non, le fou n’a rien pris en d6, contrairement à ce que je pensais initialement.
|
|
|
hommage à Beyoncé : qui a le trait ? l'échiquier est-il dans le bon sens ?
|
|
|
Beaucoup de choses ont déjà été dites, donc j'espère ne pas gâcher le plaisir de ceux qui veulent résoudre eux-mêmes : arrêtez votre lecture là.
Il y a sur l'échiquier quinze pièces blanches et six noires. Les pions blancs sur la moitié droite de l'échiquier ont capturés neuf fois pour atteindre leur position. Il reste donc une pièce blanche et une pièce noire dont on ne sait pas encore où elles ont disparues. Cela implique que le pion blanc b cinq (j'essaye de ne pas mettre de chiffre qui pourrait attirer l'œil de ce qui veulent résoudre), n'a jamais pu capturer. Du coup, le pion noir b deux ne peut atteindre sa position qu'après la seule capture noire, il vient donc de la colonne a. Le pion noir b ne peut que avoir été capturé sur sa colonne.
Le dernier coup noir ne peut donc pas être une capture du pion h trois. Le dernier coup ne peut pas non plus avoir été joué par le roi noir, ni venant de c quatre, où il aurait été en contact du roi blanc, ni venant de a quatre, à cause de l'échec double inexplicable.
Si les noirs ont joués le dernier coup, ce qu'on suppose toujours être le cas tant qu'on ne peut pas prouver le contraire, ils ont donc avancé de deux cases leur pion c, et la prise en passant est possible et elle donne mat.
L'autre intérêt de la position, c'est l'image visuelle que font les pièces sur l'échiquier. Sur la partie gauche, il y a le caractère dièse, et la colonne de pion sur la colonne h forme le chiffre un. Ce qui correspond à l'énoncé #1, qui signifie mat en un coup.
Merci d'avoir partagé ce joli petit problème.
|
|
|
Des indices vers la solution, je crois:
* Il y a 15+6 pièces au diagramme, il manque le fou blanc de cases claires.
* Les problèmes scaccograhiques ont un symbole représenté par les pièce sur l'échiquier.
* C'est en fait un problème d'analyse rétrograde, on peut déterminer les 3 derniers coups simples.
* Combien de captures ont été faites par les blancs?
* Les pions blancs des colonnes a et b ont-ils pu capturer? Que peut on en déduire pour le pion noir b2? (et incidemment pour le PNh?)
* Donc, comme le symbole scaccographique semble indiquer que le trait est au blanc, quels sont les derniers coups?
* Quelle est la réponse au symbole scaccographique?
|
|
|
Effectivement, on peut trouver les trois derniers demi-coups (c’est l’antépénultième qui m’avait échappé dans un premier temps, sans sortir l’échiquier).
|
|
|
Cette position est totalement extravagante et pourtant on ne peut s'empêcher de la décortiquer pour en comprendre les ressorts secrets..
Si je comprends bien...il serait possible par des coups légaux depuis la position de départ du jeu d'arriver à cette position ??? Alors là je suis complètement ébahi les yeux écarquillés devant l'échiquier et je me dis que j'ai besoin de quelques milliards de neurones supplémentaires pour retrouver le fil des coups joués...
|
|
|
Ah ben dis donc... Là je rentre et je viens d'apprendre quelque chose ! Scaccographique ! ( Je croyais que c'était juste un jeu de mot ).
|
|
|
@ FPC, le 18/02/2022 17:01
''Et non, le fou n’a rien pris en d6, contrairement à ce que je pensais initialement''.
Pourquoi pas ? Pas un pion, mais une tour par exemple. Non ?
|
|
|
Comme je l’ai écrit, toutes les pièces noires ont été prises par les pions blancs, sauf le pion noir de la colonne b.
Il n’y a donc pas de pièce noire disponible pour être prise en d6, ce qui fait que le fou d6 n’a pas bougé au dernier coup. C’est ce qui permet de trouver le dernier coup blanc (et l’avant-dernier coup noir).
|
|
|
Oui j'ai déjà vu ça ( ce dernier coup blanc possible rendant l’avant-dernier coup noir possible aussi ). Mais c'est l'histoire des neuf prises et du matériel subsistant qui me pose problème.
|
|
|
Si les pions blancs ont pris 9 fois ( comme lu plusieurs fois ), par exemple 5 pions + 1 fou + 2 cavaliers + 1 dame, il reste encore une seconde tour à prendre ? Donc je pourrais jouer, par exemple, 1.Fg7-f8+ Tg6-d6. Non ?
|
|
|
Non, la réponse a déjà été donnée (17:00). Le pion noir b7 a été capturé sur sa colonne (il n’a pas pu se promouvoir), et les pions blancs ont capturé les neuf autres pièces manquantes.
|
|
|
''Non, la réponse a déjà été donnée (17:00)''.
Oui, mais je peux ne pas la comprendre. J'suis un peu bête...
''Le pion noir b7 a été capturé sur sa colonne (il n’a pas pu se promouvoir)''.
Oui. Je n'en doute pas. Mais je ne vois pas trop le rapport avec ma question.
''les pions blancs ont capturé les neuf autres pièces manquantes''.
Oui. Mais j'en compte dix. A tort probablement. Mais cela me serait bien utile pour comprendre. Car autrement je crois que 16 - 9 = 7 et pas 6
( matériel noir subsistant sur l'échiquier ).
Donc pourquoi la position initiale ne pourrait-elle provenir de cette position là ? (diagramme). Dans cet ordre de coups ? Merci d'éclairer mes lumières.
1.Bf8 Rd6+ 2.Bxd6 b2 3.Nb3+ c5

|
|
|
@Chemtov : il y a 6 pièces noires sur l'échiquier. 9 pièces noires ont été prises par les pions blancs. Le pion noir B n'a pas pu capturer de pièce, n'est donc pas allé à promotion, et a donc été pris sur sa colonne. Le total est 6 + 9 + 1 = 16. Il n'y a donc plus aucune pièce noire disponible pour être capturée ailleurs.
|
|
|
Ah. Ok. Parce que moi j'incluais la disparition du pion noir dans les prises blanches ( c4xb5 ). Et j'étais trop fainéant pour compter les prises ( pas dans ma formation de joueurs d'échecs ! )
|
|
|
Le pion blanc c se trouve en e5 au diagramme (à cause d'une histoire de triangle que les joueurs d'échecs maîtrisent sûrement pour savoir si un roi peut empêcher la promotion d'un pion). S'il y avait eu c4xb5, il aurait fallu une prise supplémentaire bxc, mais ce n'est pas possible parce qu'il n'y a pas assez de pièces noires manquantes.
Si on suppose qu'il y a une pièce noire de plus qu'on puisse capturer, il y a d'autres hypothèses possibles. Par exemple que les blancs aient joués bxa (le pion noir d'origine en a7 par exemple) et axb, et le pion noir en b2 vient de b7 sans capture. Nous avons alors une pièce blanche dont on ne sait pas dire où elle a été capturée, et on peut alors imaginer que le dernier coup noir est g4xh3. Le décompte des captures blanches est souvent lié à celui des captures noires.
Faire le compte des captures est le B-A-BA en rétro. D'ailleurs il faudrait systématiquement inclure le compte des pièces présentes au diagramme sous chaque diagramme ayant un contenu rétro. En plus de faciliter le travail de ceux qui cherchent à résoudre, ça permet une vérification simple qu'il n'y a pas d'erreur au diagramme.
|
|
|
Je me souviens avoir composé la scaccographie ci-dessous (quel mot, bravo Alain !) il y a une dizaine d'années, sans autre légende que le diagramme lui-même (comme chez Andrew, mais son problème est beaucoup plus intéressant que le mien, lequel est ici assez « plat » et sans contenu rétro).
|
|
|
ok, ici un mat en 3 ;-)
Scacco... quel mot ! Alain ??
|
|
|
@thierrycatalan, une manière légale mais sûrement pas la plus rapide d'arriver à cette position de manière légale :
1. e3 a5 2. b4 a4 3. Bc4 h5 4. Bb3 axb3 5. Ne2 f5 6. Nd4 f4 7. exf4 g5 8. fxg5 Nh6 9. gxh6 h4 10. g3 h3 11. f3 e5 12. Qe2 b6 13. Nc3 Bb7 14. Kf2 Be4 15. Ke3 Bf5 16. b5 Bg4 17. fxg4 Na6 18. Ba3 Nc5 19. Bb4 Ne6 20. a4 Ng7 21. a5 Nh5 22. gxh5 Qh4 23. gxh4 Rg8 24. Ra3 Rg3+ 25. Kf2 Re3 26. dxe3 d5 27. Nf5 d4 28. Nd5 Kd7 29. c3 Ke6 30. cxd4 Bc5 31. dxe5 Bd4 32. Kf3 Rg8 33. Rc1 Rg1 34. Nc3 Re1 35. Nb1 Rd1 36. Rc6+ Kd5 37. Rxb6 Rd3 38. Nc3+ Kc4 39. Bd6 Bc5 40. Ng7 Bd4 41. Ne6 Bc5 42. Qd2 Bd4 43. Ke4 Bc5 44. Kf5 Bd4 45. Kf6 Bc5 46. Ke7 Bd4 47. Kd7 Bc5 48. Kc6 Bd4 49. Nc5 Kb4 50. Kd5 b2 51. Nb3+ c5 52. bxc6# *
Effectivement 9 prises avec les pions blancs, et la 10ème forcément le pion b noir avec une pièce blanche, comme expliqué par @Orion
|
|
|
Merci à Orion et à tous ceux qui ont expliqué la solution mieux que je n'aurais su le faire moi même! :-D
On trouve le terme Scaccographique depuis assez longtemps je crois, par exemple "Recueil de Problèmes Scaccographiques et autres positions curieuses, I. Shumov 1867" dont on parle ici...
|
|
|
Ref jetv. Merci beaucoup pour la solution du déroulé de la partie...j'avais bien essayé...mais après presque 2 heures de manipulation des pièces sur l'échiquier...j'avais renoncé..n'arrivant à rien de correct.
Je suis vraiment impressionné par cet exercice résolu.
|
|
|



