|
| Le Zéro et l'Infini aux Échecs. par MarcGelly1 le
[Aller à la fin] |
| Etudes | |
Une Etude de fin de partie,c'est LE ZERO ET L'INFINI ! La position de l'Etude proposée par le compositeur exige une partie justificative dans laquelle,forcément,le niveau de jeu est pitoyable:ZERO.
Mais ce Zéro obligé prépare la divine perfection du jeu dans la solution, voire la magie!On touche l'Infini.
La transition instantanée entre le Zéro et l'Infini fait que dans chaque Etude,on dépasse la vitesse de la lumiere!Seuls les mathématiciens savent faire celà...Un argument supplémentaire pour considérer les Echecs comme une branche des mathématiques.
MarcGelly1
|
|
|
Pourquoi la position d'une étude viendrait forcément d'une partie justificative? Il y aurait probablement une façon d'atteindre certaines études via une partie de très haut niveau. Et sinon je vois pas l'idée du post ou de son intérêt.
|
|
|
Je ne saisis pas trop, non plus, le sens de cette réflexion quasi métaphysique sur le Zélo et l'Infini. Mais provenant d'un problémiste émérite (https://www.arves.org/arves/index.php/en/latestnews/1493-gelly-marc-1937), je m'abstiens de juger (ce que je ne comprends pas).
A noter que Marc Gelly est toujours affilié à la FFE, à 87 ans ! (Membre du club Lyon Echecs passion 64).
En 1958, lors des Championnats de France (remportés avec 7,5/9 par Claude Lemoine et papa Roos), M.Gelly a terminé second de la section ''Universitaire'' devant un ex-forumeur de FE, Oroy (Caminade) et aussi devant Huguet.
Cela se passait au Touquet (http://heritageechecsfra.free.fr/1958.htm);
|
|
|
J'ai dû passer plus d'heures de ma vie à faire des mathématiques qu'à jouer aux échecs...
Je comprends le // que fait l'auteur car il y a indéniablement une ( petite) part de logique mathématique et de geometrie dans la résolution de certaines positions d'échecs, comme des " lignes " de force plus ou moins symétriques ( souvent des diagonales ! Rires).
Par contre je trouve que le jeu d'échecs est bien plus honnête intellectuellement que les mathématiques et respectueux d'une certaine vérité de la realité , car il est régi par des règles immuables ....sur un échiquier en 2 dimensions.
Cela est loin d'être le cas des mathématiques...oû l'on se permet à volonté de tricher et violer les règles du bon sens en créant ou imaginant des outils imaginaires extradimensionnels invraisemblables pour contourner un problème insoluble dans notre réalité humaine. Certaines mathématiques sont une imposture intellectuelle ..plus proches d'un mensonge et d'un travestissement de notre réalité qui est toujours vérité humaine en fin de compte.
|
|
|
@ArKheiN: tout à fait d'accord! Certaines études sont tirées de parties d'ailleurs.
@thierrycatalan: je ne comprends pas votre sortie sur les mathématiques. Il ne me semble pas que la triche soit possible en Mathématiques, les règles sont fixées au départ (les axiomes) puis on ne déroge jamais à ces règles. Vous auriez un exemple précis pour étayer votre thèse?
Quand à "Violer les règles du bon sens", les mathématiques ne prétendent pas être la réalité. Elles disent juste: "si je fixe ces règles, qu'est ce que je peux en conclure".
Certaines parties de Mathématiques sont utilisées, voire créées, pour modéliser la réalité par d'autres scientifiques (physiciens, chimistes, biologistes, etc...) qui, dans leur recherche d'un modèle cohérent avec les observations, peuvent en tester de nombreux qui mettent notre compréhension à rude épreuve (Par exemple je ne comprends pas la dualité onde/corpuscule de la lumière).
Mais ce ne sont pas les mathématiques qui sont en cause, et il faut ces étapes de tatônnements pour modéliser le réel, trouver rapidement le bon modèle n'est en général pas simple.
|
|
|
@Abrobecker
N'est ce pas un préalable indispensable pour une Étude que la position de départ puisse être obtenue par un jeu légal depuis la position initiale du jeu, contrairement aux Problèmes ?
C'est ainsi que j'avais compris le post, et son enthousiasme.
Sinon, "trouver rapidement le bon modèle n'est en général pas simple."
Et oui, et ce sera d'autant moins simple qu'on se limitera à ses perceptions et son "bon sens".
Ainsi va la science 😊
|
|
|
L'idée principale révélée par "Le Zéro et l'Infini aux Echecs"est de montrer que dans les Études dites artistiques, les merveilles, les finesses,voulues et produites par le compositeur, pour la réjouissance des connaisseurs,ne peuvent seulement surgir,dans la logique et les règles qui sous-tendent le combat échiquéen,qu'après une séquence calamiteuse d'enchainements de bourdes et de coups ineptes :La partie justificative prouvant la légalité exigée pour la position de l'étude.
Cette philosophie de L'Echiquier est probablement transposable dans notre univers spatio-temporel:
-Après la pluie,le beau temps.
-Sur le fumier poussent les plus belles plantes.
-Dans les rochers de la haute-montagne percent les fleurs aux couleurs les plus vives.
Vous en trouverez d'autres...
Bien clairement,le post ne traite pas des positions didactiques,souvent présentées comme des études (telles celles de Philidor,Lucena...)à caractère technique,d'un grand intérêt pour la théorie des finales.
Merci à Chemtov pour l'évocation du championnat de France 1958 au Toucquet.Je me rappelle bien de Michel Roos...Que de souvenirs...
|
|
|
Mais d'où sort cette idée de "partie justificative" comme préalable à une étude (oui, désolé, avec é minuscule)? Sauf dans des positions très spécifiques (avec beaucoup de matériel), on n'a pas besoin de prouver grand chose et encore, dans ces cas, "prouve"-t'on juste que la position est légale en comptant les captures...
Quant à "Après la pluie, le beau temps" et au reste, peut-être pourrait-on le laisser à Thierry Catalan et à son "bon sens" ? Chemtov et la métaphysique vont être déçus.
|
|
|
@Julo62: on souhaite aussi que la position d'un problème soit légale, sauf cas particuliers comme les problèmes féeriques (ou les compositeurs de problèmes "trichent" pour reprendre le vocable de Thierry Cathalan) ou une idée non réalisable autrement. Ce n'est pas réservé aux études...
@MargGelly1: "l'Etude proposée par le compositeur exige une partie justificative dans laquelle,forcément,le niveau de jeu est pitoyable"
Forcément? Pourquoi ne pourrait-on pas obtenir la position de certaines études après une belle partie?
Plus précisement, comme pour tout jeu combinatoire il existe une ou plusieurs lignes de jeu parfaites. Il est fort probable que certaines de ces lignes de jeu aient des positions dignes d'une étude, non?
|
|
|
En me relisant je m'aperçois que j'ai fait beaucoup de raccourcis qui peuvent rendre mes propos " bizarres" .
Je ne répéterais pas tout le plaisir que j'éprouve à jouer aux échecs ..(même face à
ceux sur internet qui me font jouer contre leur ordinateur plutôt que contre un pauvre humain comme moi...) .
En ce qui concerne les mathématiques, j'ai pu découvrir et apprécier dans mon doctorat de chimie physique toute leur utilité et même leur beauté pour expliquer les phénomènes les plus merveilleux en biologie (génétique) , en physique (fabuleuses équations de Maxwell) !, en chimie des polyméres etc.
Mais il existe des " mathématiques " ne servant rien d'autre que les mathematiques ...et qui à mon sens n'ont plus aucun lien avec le monde et la réalité qui nous entoure... ce sont ces mathématiques là qui m'ont écœuré et fait souffrir (ah je me souviens d'une démonstration immense sur un tableau noir pour arriver à 0 = 0 sous le sourire narquois du professeur de maths ...)
|
|
|
@Abrobecker
Merci 😊
|
|
|
Quant au titre du roman de Koestler (on n'est plus à une digression près), j'aurai appris à cette occasion qu'en français, il ne traduit pas littéralement le titre anglais (Darkness at Noon) qui, lui-même, transcrivait à peu près l'allemand Sonnenfinsternis (Eclipse solaire).
|
|
|
Sinon, pour en revenir au sujet, il y a autre chose qui laisse songeur : "dans chaque étude, on dépasse la vitesse de la lumière". "Chaque étude"... Il existe dans les 100 000 études publiées : parmi elles, combien de médiocres et de mauvaises ? Enormément. Même dans un championnat du monde où les compositeurs participants sélectionnent leurs meilleures compositions, certaines d'entre elles repartent avec un... zéro pointé (0/4, la moyenne tournant autour de 2/4). Pour l'infini, il faudra repasser...
|
|
|
@thierrycatalan: vous reprocher à certains pans des Mathématiques de n'être pas utiles.
Tout d'abord ce n'est pas si simple, par exemple l'étude des nombres premiers fut longtemps considéré comme un passe-temps futile de Mathématicien avant que l'on découvre leur intérêt pour la cryptographie.
Ensuite vous admirez les échecs, quel est leur utilité? Le lien avec le monde qui nous entoure?
Vous parlez de triche en Mathématiques (??), sous-entendez leur malhonnêteté, mais le seul exemple vague que vous fournissez est celui d'une démonstration scolaire qui vous a fait souffrir??
Les différentes branches des Mathématiques (j'inclus la statistique mais pas les statistiques) sont parmi les rares domaines dans lesquels on peut parler de vérité. Justement car on n'étudie pas le monde réel.
Bref, sous-entendre que les mathématiques sont malhonnêtes ou sans lien avec le monde réel me parait vraiment peu judicieux.
|
|
|
"Le Zéro et l'Infini aux Échecs".Je m'en explique tout carrément.Pour chaque étude composée digne de ce nom,avec ses pointes surprenantes,ses enchaînements raffinés de coups uniques,il existe,de facto,au moins une partie aboutissant à la position de cette étude.
Et les joueurs (fictifs) de la partie (pouvant être nommée "justificative" puisqu'elle prouve éventuellement la légalité de la position),d'après ce qu'ils montrent,possèdent un ELO égal à Zéro ! (Voire négatif ?)
Quand ces mêmes joueurs sont acteurs dans la "Solution",celui qui satisfait à la stipulation de l'étude,voit instantanément son ELO tendre vers l'Infini!Cette progression vertigineuse suggère un dépassement de la vitesse de la lumière. (De quoi éclipser les performances si remarquables des jeunes champions indiens!)
Mais l'essentiel réside dans le message offert au moyen de l'Art séculaire des compositeurs d'études :Organiquement, sur l'Échiquier avec sa géométrie et ses lois,à une longue période de mouvements désastreux,de chaos,de stratégies lamentables,peuvent succéder la virtuosité, l'harmonie,la pure félicité (NADI ANANDA).
Des lors l'univers échiquéen confirme l'antique aphorismes d'espoir :D'un mal peut surgir un bien.
|
|
|
"Un point d'exclamation qui s'est avachi donne un point d'interrogation." Tout carrément !
|
|
|
Une formulation concise pour exprimer "Le Zéro et l'Infini aux Échecs" serait :
Le niveau de jeu Zéro est nécessaire dans une partie d'échecs aboutissant à la position d'une étude dont le niveau de jeu tend vers l'Infini.
Conjecture ? Non ! Déjà "théorème échiquéen",confirmé par l'inlassable labeur de générations de compositeurs.Talentueux,voire géniaux,ils ont constitué un patrimoine multi-séculaire d'études,lesquelles révèlent cette singularité sur l'échiquier.
Un parallèle s'impose avec le saisissant changement survenant dans l'évolution du cosmos:au chaos initial s'est substituée l'harmonie transcendante de l'Univers gravitationnel d'Einstein.
Le rapprochement entre L'Échiquier et la Nature n'a rien d'étonnant.Ce n'est qu'une conséquence du principe antropomorphique, appliqué deux fois à l'envers:L'Homme est un produit de l'Univers et c'est l'Homme qui a créé L'Echiquier.
|
|
|
Là, je ne vois plus guère que l'excuse de majorité.
|
|
|
Dieu a fait émerger l’homme de l’univers.
L’univers a fait émerger l’échiquier de l’homme.
L’homme a fait émerger la beauté de l’échiquier.
L’échiquier a fait émerger les immortels de la beauté
Tout est, est source, est cause.
Mais cause toujours, se pose
que l’absence de source est
l’anéantissement de lai.
|
|
|
Moscou 1937
Dans un régime communiste, l'individu est zéro, et le Parti, c'est l'infini. Roubatchov le sait...
Ainsi démarre la 4° de couverture du livre. Il faut dire que quand j'entends ou quand je lis "toucher l'infini" je sors mon Nicolas Bourbaki (pas très pratique à l'usage ici) ou bien mon Koestler. C'est fait.
Mais au fait où sont les échecs dans son célèbre ouvrage ?
Editions Calmann-Levy
Page 100:
A part eux deux, il n'y avait dans la cantine que trois officiers assis à une table à quelque distance; deux d'entre eux jouaient aux échecs, le troisième les regardait
Page 104:
Les deux joueurs d'échecs à l'autre coin de la salle renversèrent leurs pièces et recommencèrent une partie.
Page 187:
Il avait collaboré avec lui dans ses travaux historiques; il était aussi son partenaire aux échecs et peut-être son seul ami intime.
Inutile de me raccompagner.
|
|
|
Résumons.Un grand nombre des Études dans la base (☆) vérifient le théorème "Le Zéro et l'Infini aux Échecs".La troublante analogie avec l'évolution de l'ordre dans l'histoire du Cosmos tend à l'évocation du principe antropomorphique.
N'allez pas croire que ceux qui admettent le théorème tombent parmi les aficionados du principe. On reproche au principe antropomorphique de poser un obstacle à toute Recherche.Foin d'un tel effet !Projetons toujors la composition de belles études. Ça aussi, c'est de la Recherche.Ce n'est pas seulement gagner des prix dans les concours internationaux,mais en outre,pour nous ėchėphiles,respecter le théorème et surtout créer du bonheur.
☆ ARVES CHESS.Base mondiale des études :Harold van der Heijden. Environ 100000 études à ce jour!Regarder en priorité les Prix,les Mentions d'Honneur,les Recommandées.
|
|
|
La vision antropomorphique est nécessairement un filtre à l'appréciation que nous pouvons avoir de la beauté d'une étude, qu'elle soit ou non primée.
Il me semble que j'aurais tendance à trouver belle une étude d'échecs dont je comprends la finalité, qui m'a donné du fil à retordre pour en découvrir les cases cachées de l'échiquier qui deviennent lumineuses une fois la solution trouvée....
Mais si je suis devant l'échiquier devant une position qui reste désespérement silencieuse à mes tentatives de dialogue imaginaire avec les pièces de bois, si je ne trouve pas la moindre trace d'un chemin (ou d'une impasse !) menant à l'issue de secours qui débloquera la solution de l'étude, alors je risque fort de ne pas trouver l'étude " belle" , mais stérile et sans émotions. (et hélas je suis un piètre joueur d'échecs et donc un quasi aveugle devant l'échiquier!)
C'est là tout le drame de l'homme devant l'univers ... nous n'apprecions pas la beauté de ce que nous ne voyons pas ou ne comprenons pas !
|
|
|
Toujours aussi abscons! On peut corriger quand même dans ce gloubi-boulga quelques points factuels: la base de données de Harold van der Heijden est payante (près de 100 000 etudes, ça, c'est bon) et donc on ne la trouve pas sur le site arves.org qui est un site d'informations (sur les études), site à part avec, notamment, la publication rapide des jugements de concours, géré par une autre personne, ce qui n'empêche pas HvdH d'en être membre. Il existe aussi une base de 33 000 études environ, principalement des études récompensées dans des concours, en accès libre, établie par Serhiy Didukh
|
|
|
Quant au désormais fameux "principe ant...ique", aurait-il la moindre chance d'être réévalué s'il était correctement orthographié ?
|
|
|
ref Ulysse : ne vous plaignez pas de l'orthographe!! rires... certains wokistes auraient pu écrire principe andropaumorphique limpide tout en vous qualifiant de genrophobe obscurantiste.
|
|
|
En effet,le principe anthropomorphique se défend mieux avec ses deux "h" qui lui confèrent une bonne assise.D'autant plus qu'il fût révélé par le brillant savant encyclopediste du XVIIIe :Le baron d'Holbach,lequel devait tenir à son "H".Qui plus est, le mot vient du grec.Ma conclusion:Ne pas se hâter pour simplifier l'orthographe.
Ce n'est pas le principe anthropomorphique qui est fameux mais bien le théorème "Ĺe Zéro et l'Infini aux Échecs".Fameux surtout par la mise en évidence de l'Art des Études.
Écrit déjà plus haut,nous citons à nouveau le théorème:
☆☆☆ Le niveau de jeu Zéro est nécessaire dans une partie d'échecs aboutissant à la position d'une étude dont le niveau de jeu tend vers l'Infini. ☆☆☆
Merci à Ulysse62 pour ses précisions relatives à la base d'études de Harold van der Heijden.
|
|
|
Mais que penser alors des parties de niveau de jeu très élevé (loin du Zéro) qui furent à l'origine d'études réputées ? (proches ''de l'Infini'')
|
|
|
@Chemtov
Indéniablement,des maîtres du jeu ont produit des parties générant des idées d'études qui se sont révélées fécondes.C'est au crédit de notre métier de la création artistique échiquéenne qui s'ancre ainsi d'avantage dans la réalité.Mais,en l'occurrence,ce n'est pas la transition instantanée par une position d'étude;il faut passer en travers du "réajustement" d'un compositeur. ☆ Donc c'est hors sujet.Qu'on présente un seul exemple de belle partie de maîtres "On The Board",aboutissant directement à une position d'étude qu'un juge distinguerait pour son mérite,lors il faudrait reformuler le théorème "Le Zéro et l'Infini aux Échecs ".Dans l'attente nous répétons l'intangible et quasi-organique vérité de L'Echiquier,prouvée grâce à l'immense patrimoine des Études artistiques:Par le niveau de jeu,les pures merveilles sont forcément précédées d'un noir chaos.
☆Parfois,le joueur lui-même se mue en compositeur.Exemples:Timman,Smyslov...
|
|
|
Bah... comparer la partie d'échecs et les études, cela n'a pas de sens. C'est comme comparer deux choses construites, l'une en trois dimensions, l'autre en deux dimensions (aussi belle et parfaite soit elle).. Et parler d'Elo a encore moins de sens (l'Elo mesure des résultats acquis au bout de luttes humaines, disputées dans un temps limité, dans un contexte de compétition).
Et beaucoup de finales jouées sont aussi belles et intéressantes que nombre d'études composées.
|
|
|
Personnellement, j'ai toujours pris plus de plaisir ou trouver plus beau une partie réelle qu'une étude.
Peut-être que l'étude énonce une vérité dans une position donnée, mais une partie c'est la rencontre de deux volontés, de deux individus.
Quand on joue, jusqu'au moment où on se sait foutu et qu'on continue par inertie ou pour l'équipe, on essaie de faire prévaloir son point de vue sur la position face à l'autre joueur qui fait pareil.
C'est cette confrontation que je préfère, peu importe la "vérité scientifique" du traitement de la position.
Je dirais même que, comme beaucoup, les attaques dites spéculatives de Tal sont parmi les plus beaux spectacles échiquéens dont je me souvienne. Même bien longtemps après son décès et tout seul avec un livre et un échiquier, certaines idées m'ont beaucoup marqué.
Les études, ça nous montre, peut-être, le degré de perfection scientifique que certains ont lorsqu'ils l'ont composée.
Une partie, entre joueurs de force plus ou moins égale, ça montre comment les deux protagonistes ont essayé de déjouer la stratégie et la vigilance de leur adversaire.
Et ça, je trouve que ça peut encore plus servir dans des domaines très différents des échecs. J'ai une profession plutôt "compétitive", quand on gagne une affaire, c'est bien souvent qu'un ou des autres la perdent. Les échecs n'apprennent pas à faire ça, mais le jeu réel peut permettre une comparaison pas si sotte, ama.
Pour mon cas, je pense à la prophylaxie particulièrement. C'est sans doute une qualité et un défaut de mon jeu de plus prendre en compte les possibilités adverses que les miennes. Et c'est assez transposable dans d'autres activités.
D'autre part, la partie, ce sont deux individus qui viennent s'asseoir à la table, avec leurs ambitions et leurs déceptions, leurs renoncements et leurs joies, le cour de musique du petit dernier, la promotion méritée au boulot, la grippe de grand-maman, le loyer à payer, les vacances dans pas longtemps, la révision de la clio... Mais ça joue !
Alors je conçois l'enthousiasme de l'auteur du post, mais je ne partage pas 😊
Édit : croisement avec Chemtov
|
|
|
Je précise que j'aime beaucoup les études. Et j'ai le plus grand respect pour leurs auteurs. Quant aux ''deux ou trois dimensions'', ma remarque n'avait nullement pour but de hiérarchiser le Jeu d'Echecs proprement dit (''jeu'') et la composition. Tout comme je ne compare pas une photographie de Cartier-Bresson ou un portrait de Léonard De Vinci avec un modèle vivant (être humain en trois dimensions !).
|
|
|
Pour moi on pourrait définir une position aux échecs comme ceci: photographie d'un instant T d'une partie aux échecs. On a aucun élément pour dire si ce qui a précédé était bien joué ou non, sauf si on tombe sur une position avec un gain évident avec un très gros déséquilibre matériel, on peut fortement supposer de grosses erreurs au moins d'un côté. Dans les positions des études, la situation est suffisamment complexe pour nous faire dire que ce qui a précédé a pu être très bien joué, surtout pour les études où le but est de faire nul (sans être un spécialiste, il me semble qu'il y a énormément d'études dans ce but-là). Même dans le cas d'une étude je ne vois pas comment on peut parler d'ELO Zéro, déjà, ça ne veut rien dire, le niveau le plus "nul" aux échecs, du moment qu'on considère que le(s) joueur(s) (humain, logiciel, animal, extra-terrestre, esprit, un dieu ou autre) maîtrise les règles du jeu comme comme règle minimale, le niveau le plus nul serait quelque chose proche du jeu aléatoire complet, et ne saisissant jamais les mats autorisés, alors qu'on se laisse mater/faire prendre du matériel gratuitement, ou alors jouer du f3-g4 à chaque fois sans jamais apprendre...
Donc à priori, les "joueurs" d'une étude n'en sont clairement pas à ce stade. Il me semble d'ailleurs qu'il serait très improbable de tomber sur une position d'étude réelle ou potentielle avec un jeu totalement aléatoire ou mauvais des deux joueurs.
Et même parler de chaos pour parler de la position de départ d'une étude me semble faux, même dans le cas (voire surtout?) si l'étude a été créée à partir d'un champion d'études "non joueur", je le verrais comme une sorte d'horloger ayant créé un très fin mécanisme, ou rien n'est laissé au hasard. Pourquoi parler ici de chaos?
Bref tout ça pour dire que je ne comprends pas la thèse qu'on essaie de nous vendre ici, ni de son intérêt, alors que je peux apprécier une étude et le talent créatif de celui qui l'a inventée.
|
|
|
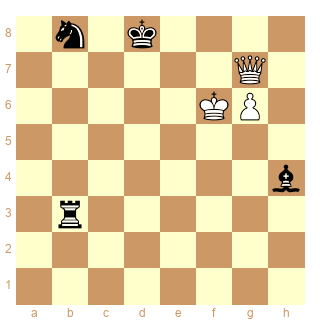
Dans cette position, générée par les tablebases, nous avons le plus long mat avec 7 pièces sur un jeu optimal des deux côtés. Les Blancs jouent et matent en 549 coups.
Si ça se trouve, la position répond aux critères de beauté ou de condition pour faire partie d'une étude, encore qu'il faut avoir du courage pour s'attaquer à ça... Pour moi, cette forme de beauté me fascine, et dans cette position particulière, on y retrouve des choses intéressantes: déséquilibre matériel, sous-promotion, balade du roi blanc, jeu précis avec la dame et cavalier, promenade du roi blanc à nouveau, etc...
Qui pourrait affirmer que le jeu qui a précédé était nul? Personne, et au vu de ma théorie du post précédent, aucun des joueurs était "nul", et il est peu probable qu'ils aient pu atteindre cette position qu'est le mat optimal le plus long en 7 pièces, par un hasard complet (question pour un statisticien/mathématicien pour la probabilité?), sachant qu'il y aurait 423836835667331 positions légales dans les tablebases 7, ça peut donner une idée...
Après oui, dans un sens, on peut dire que le créateur de ladite position: le générateur de tablebases, a un niveau zéro car il ne sait pas faire ce qui précède, et dans un sens, il ne sait pas jouer, il sait compter à la perfection/a une mémoire de 18 terabyte.
|
|
|
Un jeu amusant serait essayer d'atteindre cette position sur le jeu le "moins mauvais possible", est-ce qu'il est possible d'atteindre cette position avec un jeu qui a précédé et qui s'approche de la perfection, du moins pour le futur vainqueur? Voilà une belle question métaphysique un peu en lien à mon avis, avec l'idée de départ du post.
Tout ce qu'on sait du passé le plus proche, c'est que le fou noir était en e1/f2/g3 au coup d'avant, le plus probable est qu'il était en f2, et qu'il y avait une tour en h4 (si on veut respecter la situation la plus équilibrée), qui fait que le meilleur coup est 1..Fxh4+.
|
|
|
On peut même imaginer que les Blancs avaient une dame en h4, ce qui fait que le fou noir était peut-être bien en e1 et en g3, la position semble trop déséquilibrée pour être plausible, avec 2 dames contre 0 mais allez savoir, peut-être que les Noirs au coup d'avant venaient de jouer le meilleur coup avec ..Dh4+ ou ..Dxh4+ 1.Dxh4 Fxh4, dans tous les cas, continuer la méthode "tablebase" en partant de la fin et non du début comme une partie normale, pourrait être la meilleure façon de tenter de reconstruire la partie intégrale ayant amené cette position via le jeu le moins imparfait.
|
|
|
Il me semble que la différence essentielle entre une position issue d'une partie "réelle " et une position issue d'une étude composée est principalement le TEMPS que le joueur peut consacrer à trouver la clef ou la "vérité " de la position...
Dans une partie réelle disons de 40 coups, on a en moyenne 3 minutes pour choisir son coup , on peut certes gérer son temps pendule et y consacrer disons 30 minutes...
Pour une étude...je suppose que l'on peut devoir aisement passer plusieurs heures d'analyses pour trouver la clef de la solution....et le coup gagnant...
A mon sens , ce n'est donc pas du tout la même façon de résoudre , ni de réfléchir sur une position donnée sur l'échiquier.
|
|
|
Je crois qu'on s'éloigne du sujet de MarcGelly1 qui est centré sur les études artistiques (avec leurs règles précises, coups uniques et autres contraintes). Enfin... je ne sais pas... peut-être...
Est-ce que les études de finale (pas forcément ''artistiques'') tendent vers ''l'Infini'' ? Mystère...
En tous les cas, il existe des finales d'une complexité incroyable, produites par des humains, en parties réelles (souvent de bonnes parties, loin du ''Zero'' et du ''Chaos'') qui égalent facilement les études composées.
Depuis quelques temps, j'essaie ainsi de comprendre les finales de fous de couleurs opposées. Le livre ''The secrets of the Opposite-Coloured Bishop Endings'' de Gyula Meszaros est un bon support qui présente parties et études composées (ou finales théoriques ? sont-ce des études ? il est noté ''study'' même si la ''règle'' sur les coups uniques n'est pas toujours respectée) (donc l'Infini s'éloigne peut-être...)
|
|
|
Celle-là est infernale (Partie Kaidanov-Antoshin, Bryansk 1984). Rien à envier aux études de Horwitz, Herbstmann, Bondarenko, Chekhover, etc... sur le même sujet.

|
|
|
Bon... Dans Averbach, il y a pire... Avec la finale (aussi de fous de couleurs opposées) entre Henkin et Dubinsky, sur six pages, nécessitant treize diagrammes!
|
|
|
Ce qui m'étonne, ce qu'on en soit encore a chercher s'il y a quelque chose de défendable derrière les termes de Zéro et d'Infini et dans le soi-disant théorème... Il y a quelques années, on aurait crié au bon vieux troll (bon d'accord, l'âge vénérable de l'inventeur n'y incite en principe pas...). J'ai composé plus de 400 études (dont environ deux cents récompensées dans des concours), rédigé des centaines de pages d'articles sur les études de dizaines de compositeurs, et je n'ai jamais entrevu nulle part la moindre ombre de noir chaos au moment de composer (en revanche, un petit bonjour à Nyarlathotep, le chaos rampant, où qu'il soit..
, il s'y connaissait en etudes) ni n'ai senti sur moi le souffle mystique de l'infini (ni celui de soi-disant Vérité), je dois vraiment être trop prosaïque pour ces hautes considérations...
|
|
|
Bah... MarcGelly1 a apporté un peu de poésie dans notre monde sévère. Troll ? Non. Mais peut-être pataphysicien (j'ai cru d'abord métaphysicien) inspiré par ''Gestes et opinions du docteur Faustroll, pataphysicien''(roman ''néo-scientifique'' d'Alfred Jarry).
|
|
|
Pataphysique consciente ou inconsciente?
Celle de Jarry, des patacesseurs ou celle du Collège ?
|
|
|
@Ulysse62: Oui, arrêter de chercher un sens au propos de certains semble judicieux.
Comme j'ai parlé de vérité, en Mathématiques, je me permets toutefois de réagir auprès de l'expert en finales que vous êtes: les tables de finales ne fournissent-elles pas la vérité?
|
|
|
"Expert en finales", moi, non, sûrement pas. Mais pour quelqu'un qui l'est, oui, les positions en 6, 7 pièces et bientôt les 8 sans doute, donnent la matière pour cartographier le terrain et connaître les moindres détails de finales avec un matériel donné, si seulement cela est possible au cours d'une vie. Le compositeur d'études n'a pas, sauf exception, de volonté d'exhaustivité, mais il va emprunter, éventuellement, ponctuellement (sauf ceux qui ne composent qu'en 6 ou 7 pièces), tel ou tel segment d'analyse aux egtb, pour s'en servir comme élément de sa propre composition. Avec l'assurance de la correction. Mais la "vérité" artistique n'est pas forcément superposable à la vérité tout court.
|
|
|
Bon... j'espère que nous n'avons pas froissé MarcGelly 1... (c'est le risque de visiter ce monde de brutes insensibles).
A l'occasion, je vous donnerai la solution du diagramme que j'ai mis (Erony m'en a envoyé une autre, encore plus gratinée, toujours avec fous de couleurs opposés) (aussi une partie, pas une étude).
|
|
|
"Le Zéro et l'Infini aux Échecs" se heurte à un mur d'incompréhension. Déception,certes,mais pas une surprise! Cas infime en regard de grands précédents:Galilée,"Et pourtant,elle tourne"-Semmelweis et la fièvre perpuerale...
Il faut répéter,récapituler,puisque personne n'écoute.
La proposition est un théorème. Elle s'appuie sur un raisonnement logique utilisant des faits donnés et des hypothèses incontestables.
LEMME 1- Le niveau de jeu montré par un joueur d'échecs,réel ou fictif,dans des parties d'échecs,est caractérisé par un chiffre. Exemples:J.R. Capablanca jouait à 2××× - Stockfisch 16 joue à 3××× ...
LEMME 2- Dans la solution d'une étude artistique,l'enchaînement miraculeux de "coups uniques",comme l'exige la règle régissant toute composition,correspond à un niveau de jeu qui tend vers l'Infini.
LEMME 3- Toute position d'étude devant être légale,il existe au moins une partie aboutissant à cette position.C'est une suite de coups plus ou moins ineptes,ne pouvant se traduire que par un niveau de jeu Zéro.
La juxtaposition logique des LEMMES 1,2 et 3 permet d'ennoncer le théorème.
CE QUE LE THÉORÈME N'EST PAS.
La progression de Zéro à l'Infini du niveau de jeu n'est que théorique. Elle ne peut constituer l'exemple inaccessible générateur d'une vague de découragement.Tout joueur d'échecs s'interdira d'être submergé devant la vanité d'un quelconque effort et poursuivra son travail patient pour progresser dans sa compréhension du jeu.
CE QUE LE THÉORÈME EST.
La révélation d'un phénomène transcendant par le biais de l'Étude Artistique.L'élévation instantanée, la plus fulgurante possible, du niveau de jeu est un coup de projecteur providentiel sur notre art pourtant multi-séculaire. Il en a terriblement besoin.
CE QUE LE THÉORÈME POURRAIT ÊTRE.
L'Étude Artistique, avec ses règles si précises. si contraignantes,est greffée sur le jeu d'échecs dont les conventions sont elles-mêmes très arbitraires. Tout cela est voulu et issu de l'esprit humain.Et l'aboutissement (☆) est ce phénomène inouï qui nous interroge.Des générations de chercheurs se pencheront sur la question...Voltaire attend peut-être les thèses...
(☆) outre qu'il nous enseigne que sur l'échiquier. les merveilles sont nécessairement précédées d'une période calamiteuse.
|
|
|
Mais, vous savez, moi je ne crois pas qu’il y ait de bonne ou de mauvaise situation.
Moi, si je devais résumer ma vie aujourd’hui avec vous, je dirais que c’est d’abord des rencontres, des gens qui m’ont tendu la main, peut-être à un moment où je ne pouvais pas, où j’étais seul chez moi. Et c’est assez curieux de se dire que les hasards, les rencontres forgent une destinée…
Parce que quand on a le goût de la chose, quand on a le goût de la chose bien faite, le beau geste, parfois on ne trouve pas l’interlocuteur en face, je dirais, le miroir qui vous aide à avancer. Alors ce n’est pas mon cas, comme je le disais là, puisque moi au contraire, j’ai pu ; et je dis merci à la vie, je lui dis merci, je chante la vie, je danse la vie… Je ne suis qu’amour !
Et finalement, quand beaucoup de gens aujourd’hui me disent : « Mais comment fais-tu pour avoir cette humanité ? » Eh bien je leur réponds très simplement, je leur dis que c’est ce goût de l’amour, ce goût donc qui m’a poussé aujourd’hui à entreprendre une réflexion philosophique, mais demain, qui sait, peut-être simplement à me mettre au service de la communauté, à faire le don, le don de soi…
|
|
|
Je me demande si Galilée aurait lui aussi confondu chiffre et nombre?
L'ensemble du texte est à l'avenant.
|
|
|
De toute façon, pour la médaille Fields, la limite d'âge était (largement) dépassée.
|
|
|
C'est dommage que chaques interventions de M.Gelly soient un ensemble d'affirmations tel un exposé sans débat possible, ne tenant pas compte des avis différents du sien. Rien que l'énoncé "hypothèses incontestables" est agaçant et contestable pour des raisons déjà évoquées par les répondants.
|
|
|
Convoquer Galilée et Semmelweis était pourtant prometteur.
Cela dit nul n'est jamais certain de pouvoir résister à l'hybris, il m'arrive même parfois d'invoquer Anish Giri c'est dire...
|
|
|
@ Marc Gelly : votre theoreme n’a aucun sens car il n’y a aucune raison que la proposition « C'est une suite de coups plus ou moins ineptes, ne pouvant se traduire que par un niveau de jeu Zéro. » du lemme 3 de votre dernier post soit juste.
« Mathematiquement », en resolvant le jeu d’echecs on constaterait qu’un jeu parfait des deux joueurs aboutit necessairement a un resultat donne (aujourd’hui nos connaissances et les ordinateurs ne suffisent pas encore pour déterminer si ce resultat est une victoire des Blancs ou une partie nulle, mais on peut sans doute affirmer qu’il ne s’agit pas d’une victoire des Noirs)
Ainsi tout coup qui ne change pas l’evaluation de la partie (soit gain force des blancs quel que soit le jeu des Noirs, soit nulle sur un jeu parfait des deux joueurs) peut être considere comme un coup parfait.
Donc si par exemple le resultat d’une partie parfaite doit aboutir a la nulle : si l’intitule d’une etude est « Les Blancs jouent et gagnent » cela signifie que les Noirs ont fait au moins une erreur. Cependant si l’intitule est « Les Blancs jouent et font nulle » il n’y a aucune raison a priori qu’on ne puisse pas atteindre la position de base de l’etude avec un jeu parfait, au sens ou l’evaluation reste « nulle » tout au long de la partie.
|
|
|
@Map171717 : En quelque sorte, vous semblez nous dire que toute étude artistique, avec la légende ''Les blancs jouent et gagnent'' serait probablement le résultat vicié d'une partie parfaite, dont le résultat normal aurait du se retrouver dans une position de roi contre roi.
Je ne dis pas la ''fin'' normale car MarcGelly nous parle d'Infini. Car seules les règles humaines (répétitions de positions, cinquante coups, etc...) pourront créer une fin au Jeu, gâchant arbitrairement le merveilleux ballet, perpétuel et infini, des rois.
Hélas, de vils compositeurs d'étude polluent ainsi la pureté de notre Jeu parfait (qui commençait si bien, dans la richesse et la perfection absolue de la position initiale) (qu'on ne peut qualifier de ''Zéro'') . Ces odieux personnages iconoclastes, donc, inséminent des germes de fautes dans le Jeu, des imprécisions perverses, qui développent la maladie fatale des noirs (avec toujours cette théorie raciste). Tout cela pour parvenir à une odieuse fin programmée, supposée contenir quelques aspects esthétiques.
|
|
|
Chemtov, sans rapport direct (de toute façon, dans ce post, tout est bancal...), l'article sur Febus Fraenkel est juste paru (janvier 2024 officiellement, novembre pour la diffusion)
|
|
|
Merci, Ulysse. Mais paru où ?
|
|
|
Je n'ose plus intervenir sur cette guirlande, ni sur le mode comparaison des échecs avec les mathématiques, ni sur le mode philosophique, ni sur le mode humoristique....
mais je dois quand même remercier Chemtov qui m'a fait sourire sans discontinuer durant 5 minutes dans sa réponse à map...
J'avais l'impression d'être une victime du Joker ...
Sinon l'hypothèse 1 de M. Gelly disant que Capablanca jouait à un niveau de 26xx alors que Stockfish joue à un niveau de 35xx m'interpelle ...me semble déjà "frelatée" pour reprendre un mot cher à Krusti.
Stockfish triche par rapport à Capablanca ...la "turbine" joue en consultant sa ROM et en récitant l'intégralité de la théorie des ouvertures et des finales ...élaborée par Capablanca et consors .....
Si on prive Stockfish de ses bibliothèques ouvertures et finales...en le laissant calculer seul et jouer des coups " d'amateur" il risquerait fort de se faire battre facilement par un GMI humain....
|
|
|
Avec un peu de chance, dans l'unique publication française consacrée à la composition, Phénix. Sommaire en ligne www.phenix-echecs.fr
|
|
|
LA SYNECDOQUE!Le chiffre de la population,le chiffre d affaire,une guerre de chiffres
|
|
|
Le Zéro et l'Infini aux Echecs.
C'était dans un parc urbain,sous les platanes,par une soirée d'été. Quelques échiquiers en pierre sont disposés. Deux joueurs s'installent, prêts à en découdre. Des habitués, des connaisseurs, rôdent dans les parages.En alerte, ils s'approchent. Ils sont toujours friands de situations critiques.avides de pointes réjouissantes...
Les coups surgissent,presque sans temps de réflexion.En réalité, les deux acteurs récitent une partie tendant à produire la position d'une Étude artistique!Et la consternation s'imprime sur les visages de tous les spectateurs:Quelles hideuses grimaces!Jamais,en ce lieu,ne se sont exhibées de telles "mazettes".Déjà, certains font mine de s'éloigner. Le conducteur des Noirs se lève et retient par le coude un des fuyards.
__Patience, idiot!Elles arrivent les surprises!Mais oui,on va t'amuser!
Survient le dernier coup générant l'Etude, une des plus fameuses de Genrik Kasparyan.Alors,le joueur des Blancs exécute la "clef":"A great key move"!Elle provoque dans l'assistance l'étonnement, l'incrédulité.La cadence des répliques, dans la "solution" s'est considérablement ralentie. Temps pour comprendre,savourer...Le niveau de jeu bondit prodigieusement vers l'infini!Place au festival des masques:sideration, enthousiasme, jubilation,extase...
Les deux acteurs?C'étaient Henri Rinck et Aleksei Troitzky:deux revenants,pères de l'Etude artistique moderne!Leur motivation?La mise en évidence d'un ressenti chez l'être humain du "Zéro et l'Infini aux Echecs"?Peut-être...L'effet sur les zygomatiques?Très certainement!
Témoignage presque imaginaire...
|
|
|
Ah la la... Et à côté de cela, il y a ces maudits champions d'échecs qui tentent de jouer des parties parfaites, exemptes de fautes, ultra-précises, défiant les meilleurs programmes, et qui nous privent ainsi de la production de parties horribles, de niveau zéro, mais propices à la création des plus belles études artistiques. Pfff... Quel gâchis...
Cependant, les parties parfaites des maîtres, si elles ne permettent pas de créer des positions d'étude menant au gain (car l'équilibre ne sera jamais rompu entre deux camps jouant parfaitement), elles pourraient quand même générer des études artistiques se terminant par le match nul.
La perfection absolue.
Ou de l'Infini à l'Infini... Gens una sumus... (joueurs et compositeurs)
|
|
|
je crois avoir souvent dit sur le forum , que l'appreciation de la beauté d'une partie, se juge en fonction du niveau de notre compréhension du jeu d'échecs ....
Ainsi , Kasparov va trouver magnifique des parties de Karpov que la majorité des amateurs peuvent juger " ennuyeuse avec un gain technique" ....
De même Karpov pourra juger une partie de Carlsen de 70 coups gagnée en finale de pions comme un chef d'oeuvre, alors que la majorité des commentateurs la trouve "sans relief avec des manoeuvres interminables"...
Pourtant , même à mon modeste niveau d'amateur, je suis capable de comprendre qu'il y a beaucoup de parties nulles en 40 coups , qui méritent largement d'etre rejouées et qui sont de magnifiques parties ...qui finissent par une nulle sur l'échiquier.
Dans Europe Echecs , chaque mois, toutes les belles parties ne se terminent pas toutes par 1-0 ou 0-1
|
|
|
Lu dans Europe Echecs :
D'abord : « Les études sont des positions de fins de partie avec un contenu extraordinaire ». Richard Réti
Ensuite : « On distingue les études artistiques des problèmes en fonction de trois critères :
1. La Nulle est possible
2. etc... 3. etc...»
Exercice : Comment construire une partie entière, quasi parfaite, qui mènerait, par exemple, à la fameuse étude de Reti, celle avec un pion c et un pion h (Il faudrait que Stockfish ne bondisse pas au-delà de -0,2 par coup). On arriverait alors à l'Infini / l'Etude de Reti (''Infini'' à la manière de MarcGelly1) sans passer par le ''Zéro'', en frisant en permanence la perfection (à la manière de Stockfish). Il faudrait rester dans l'égalité constante, en créant cependant de subtiles dissymétries pour obtenir progressivement, après de nombreux échanges, la finale de pions souhaitée.
|
|
|
Chemtov @29/03/2025 21:17
La proposition utilisant l'Etude de Réti (celle de 1921) vise à restreindre le champ de validité du "Zéro et l'Infini aux Echecs".Intéressant mais relève du trou de souris.Acrobatique quand on sait que le Roi blanc progresse de e1 à h8 alors que le logiciel Stockfish doit maintenir dans toute la partie sa première ligne d'évaluation à +/- 0,2.Qui plus est,certains 00 actuels de Stockfish semblent entachés de doutes.
|
|
|
@MarcGelly1 : ''restreindre le champ de validité du "Zéro et l'Infini aux Echecs" ? Disons plutôt que je propose ''0.0 et l'Infini aux Echecs'' !
|
|
|
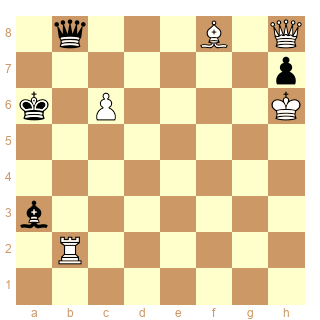
J'ai commencé à étendre l'infini précédant l'étude de Réti (diagramme ci-dessous),
1.Txb2 Fxb2 2.Fg7 Fxg7 3.Rxg7 Dxh8+ 4.Rxh8 h5
A vous d'essayer de continuer à précéder cet infini!
|
|
|
Je pense que cela va être difficile comme ça. J'imaginais plutôt de longues parties, paisibles, sans fautes, où le matériel se restreindrait progressivement, inexorablement. Et où, à un moment donné, il faudrait trouver un moment clé pour basculer dans une belle étude menant au match nul. C'est ce lien entre deux positions qui est difficile à trouver.
En revanche si l'on accepte que le 0.0 aille jusqu'à 0,8 ou 0,9 (toujours dans la tranche du 0.) on peut trouver des parties entières qui se terminent par de jolies combinaisons forçant le match nul (forme d'Infini) (l'échec perpétuel, infini, par définition). Des parties esthétiques presque parfaites.
(loin de la Partie d'Echecs vue par MarcGelly1 comme : ''une séquence calamiteuse d'enchainements de bourdes et de coups ineptes'').
|
|
|
D'abord,H.Rinck et A.Troitzky,acteurs, nous ont gratifiés sur l'échiquier d'une véritable dystopie.Leurs manœuvres aboutissent à la position d'une Étude dont la clé (KEY MOVE) provoque un phénomène inouï:instantanément,sur les 64 cases,pour les connaisseurs,c'est paradisiaque!Seule une Étude artistique permet cela.Les deux Pères dans cet Art avaient à cœur de le montrer.Ont-ils été convaincants?La mission leur incombait,donc ils étaient convaincus...
|
|
|



